题目内容
18．双曲线$\frac{y^2}{16}-\frac{x^2}{9}=1$的焦点是（0，5），（0，-5）；离心率为$\frac{5}{4}$；渐近线为y=$±\frac{4}{3}$x．分析 利用双曲线方程直接求解双曲线的焦点坐标，离心率以及局限性方程即可．
解答 解：双曲线$\frac{y^2}{16}-\frac{x^2}{9}=1$，可得a=4，b=3，c=5，则双曲线的焦点是（0，5），（0，-5）；
离心率为：e=$\frac{5}{4}$；
渐近线方程为：y=$±\frac{4}{3}$x；
故答案为：（0，5），（0，-5）；$\frac{5}{4}$；y=$±\frac{4}{3}$x．
点评 本题考查双曲线的简单性质的应用，是基础题．
练习册系列答案
天天练口算系列答案
相关题目
8．已知sinx+cosx=$\frac{1}{5}$（0≤x＜π），则tanx的值等于（ ）
| A． | -$\frac{3}{4}$ | B． | -$\frac{4}{3}$ | C． | $\frac{3}{4}$ | D． | $\frac{4}{3}$ |
9．已知函数$f（x）=\left\{\begin{array}{l}{e^{|x-1|}}\;\;，\;x＞0\\-{x^2}-2x+1\;，x≤0\end{array}\right.$，若关于x的方程f2（x）-3f（x）+a=0（a∈R）有8个不等的实数根，则a的取值范围是（ ）
| A． | $（0，\frac{1}{4}）$ | B． | $（\frac{1}{3}，3）$ | C． | （1，2） | D． | $（2，\frac{9}{4}）$ |
6．在△ABC中，角A，B，C的对边分别为a，b，c，且${cos^2}\frac{B}{2}=\frac{a+c}{2c}$，则△ABC的形状为（ ）
| A． | 直角三角形 | B． | 等腰三角形 | ||
| C． | 等腰三角形或直角三角形 | D． | 等腰直角三角形 |
13．下列各组中的两个函数是同一函数的为（ ）
| A． | f（x）=1，g（x）=x0 | B． | f（x）=$\root{3}{x}$，g（x）=$\frac{{x}^{2}}{x}$ | C． | f（x）=lnex，g（x）=elnx | D． | f（x）=$\frac{1}{|x|}$，g（x）=$\frac{1}{\sqrt{{x}^{2}}}$ |
3．已知函数f（x）=x3-12x，若f（x）在区间（2m，m+1）上单调递减，则实数m的取值范围是（ ）
| A． | [-1，1] | B． | （-1，1] | C． | （-1，1） | D． | [-1，1） |
10．
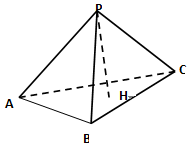已知P为△ABC所在平面外一点，PA⊥PB，PB⊥PC，PC⊥PA，PH⊥平面 ABC，H，则H为△ABC的（ ）
已知P为△ABC所在平面外一点，PA⊥PB，PB⊥PC，PC⊥PA，PH⊥平面 ABC，H，则H为△ABC的（ ）| A． | 重心 | B． | 垂心 | C． | 外心 | D． | 内心 |
7．已知$\vec a=（-1，-3，2）$，$\vec b=（1，2，0）$，则$\vec a•\vec b$=（ ）
| A． | -5 | B． | -7 | C． | 3 | D． | $\frac{1}{3}$ |
在长方体ABCD-A1B1C1D1中，AA1=AD=4，E是棱CD上的一点．