题目内容
17.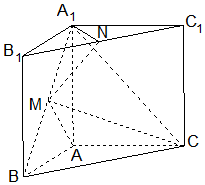 在三棱柱ABC-A1B1C1中,侧棱与底面垂直,∠BAC=90°,AB=AA1,点M,N分别为A1B 和B1C1的中点.
在三棱柱ABC-A1B1C1中,侧棱与底面垂直,∠BAC=90°,AB=AA1,点M,N分别为A1B 和B1C1的中点.(1)证明:A1M⊥平面MAC;
(2)证明:MN∥平面A1ACC1.
分析 (1)证明A1M⊥MA,AM⊥AC,故可得A1M⊥平面MAC;
(2)连结AB1,AC1,由中位线定理得出MN∥AC1,故而MN∥平面A1ACC1.
解答  证明:(1)由题设知,∵A1A⊥面ABC,AC?面ABC,∴AC⊥A1A,
证明:(1)由题设知,∵A1A⊥面ABC,AC?面ABC,∴AC⊥A1A,
又∵∠BAC=90°,∴AC⊥AB,
∵AA1?平面AA1BB1,AB?平面AA1BB1,AA1∩AB=A,
∴AC⊥平面AA1BB1,A1M?平面AA1BB1
∴A1M⊥AC.
又∵四边形AA1BB1为正方形,M为A1B的中点,∴A1M⊥MA,
∵AC∩MA=A,AC?平面MAC,MA?平面MAC,∴A1M⊥平面MAC…(6分)
(2)连接AB1,AC1,由题意知,点M,N分别为AB1和B1C1的中点,∴MN∥AC1.
又MN?平面A1ACC1,AC1?平面A1ACC1,∴MN∥平面A1ACC1.…(12分)
点评 本题考查了面面垂直,线面平行的判定,属于中档题.

练习册系列答案
相关题目
8.已知sinx+cosx=$\frac{1}{5}$(0≤x<π),则tanx的值等于( )
| A. | -$\frac{3}{4}$ | B. | -$\frac{4}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
12.已知f(x)=2sinx+cosx,若函数g(x)=f(x)-m在x∈(0,π)上有两个不同零点α、β,则cos(α+β)=( )
| A. | $\frac{4}{5}$ | B. | $\frac{3}{5}$ | C. | $-\frac{4}{5}$ | D. | $-\frac{3}{5}$ |
9.已知函数$f(x)=\left\{\begin{array}{l}{e^{|x-1|}}\;\;,\;x>0\\-{x^2}-2x+1\;,x≤0\end{array}\right.$,若关于x的方程f2(x)-3f(x)+a=0(a∈R)有8个不等的实数根,则a的取值范围是( )
| A. | $(0,\frac{1}{4})$ | B. | $(\frac{1}{3},3)$ | C. | (1,2) | D. | $(2,\frac{9}{4})$ |
6.在△ABC中,角A,B,C的对边分别为a,b,c,且${cos^2}\frac{B}{2}=\frac{a+c}{2c}$,则△ABC的形状为( )
| A. | 直角三角形 | B. | 等腰三角形 | ||
| C. | 等腰三角形或直角三角形 | D. | 等腰直角三角形 |
7.已知$\vec a=(-1,-3,2)$,$\vec b=(1,2,0)$,则$\vec a•\vec b$=( )
| A. | -5 | B. | -7 | C. | 3 | D. | $\frac{1}{3}$ |