题目内容
12．复数$z=\frac{4}{1+i}$（i是虚数单位）的共轭复数在复平面内对应的点是（ ）| A． | （2，-2） | B． | （2，2） | C． | （-2，-2） | D． | （-2，2） |
分析 利用复数的运算法则、共轭复数的定义即可得出．
解答 解：$z=\frac{4}{1+i}$=$\frac{4（1-i）}{（1+i）（1-i）}$=2-2i（i是虚数单位）的共轭复数2+2i在复平面内对应的点（2，2）．
故选：B．
点评 本题考查了复数的运算法则、共轭复数的定义，考查了推理能力与计算能力，属于基础题．
练习册系列答案
快乐5加2金卷系列答案
相关题目
3．已知函数f（x）=x3-12x，若f（x）在区间（2m，m+1）上单调递减，则实数m的取值范围是（ ）
| A． | [-1，1] | B． | （-1，1] | C． | （-1，1） | D． | [-1，1） |
20．若一个圆台的轴截面如图所示，则其侧面积等于（ ）
| A． | 6 | B． | 6π | C． | $3\sqrt{5}π$ | D． | $6\sqrt{5}π$ |
7．已知$\vec a=（-1，-3，2）$，$\vec b=（1，2，0）$，则$\vec a•\vec b$=（ ）
| A． | -5 | B． | -7 | C． | 3 | D． | $\frac{1}{3}$ |
17．已知一个几何体的三视图如图所示，则该几何体的体积是（ ）
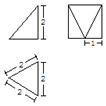
| A． | $2\sqrt{3}$ | B． | $\frac{2}{3}\sqrt{3}$ | C． | $\frac{4}{3}\sqrt{3}$ | D． | $4\sqrt{3}$ |
2．x，y满足约束条件$\left\{\begin{array}{l}{x+y-2≤0}\\{x-2y-2≤0}\\{2x-y+2≥0}\end{array}\right.$，若z=y-ax取得最大值的最优解不唯一，则实数a的值为（ ）
| A． | $\frac{1}{2}$或-1 | B． | 2或$\frac{1}{2}$ | C． | 2或-1 | D． | 2或1 |