题目内容
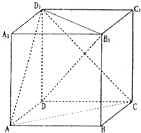 在正方体ABCD-A1B1C1D1中,给出以下结论:
在正方体ABCD-A1B1C1D1中,给出以下结论:①DB1⊥平面ACD1;
②AD1∥平面BCC1;
③AD⊥平面D1DB;
④平面ACD1⊥平面B1D1D;
⑤AB与DB1所成的角为45°.
其中所有正确结论的序号为
考点:异面直线及其所成的角,空间中直线与直线之间的位置关系,空间中直线与平面之间的位置关系
专题:空间位置关系与距离
分析:对于①,推导出DB1⊥AC,DB1⊥D1C,从而得到DB1⊥平面ACD1;对于②,由AD1∥BC1,得到AD1∥平面BCC1;对于③,由AD与DB的夹角为45°,得到AD与平面D1DB一定不垂直;对于④,由DB1⊥平面ACD1,得到平面ACD1⊥平面B1D1D;对于⑤,设AB=a,则AD1=
,BD1=
,所以AB与DB1所成的角为90°.
| 2 |
| 3 |
解答:
解:对于①,连结BD,则BD⊥AC,又BB1⊥AC,
∴AC⊥平BDB1,∴DB1⊥AC,
同理,DB1⊥D1C,∴DB1⊥平面ACD1,故①正确;
对于②,∵AD1∥BC1,
AD1不包含于平面ACD1,BC1?平面ACD1,
∴AD1∥平面BCC1,故②正确;
对于③,∵AD与DB的夹角为45°,DB?平面D1DB,
∴AD与平面D1DB一定不垂直,故③不正确;
对于④,∵DB1⊥平面ACD1,DB1?B1D1D,
∴平面ACD1⊥平面B1D1D,故④正确;
对于⑤,设AB=a,则AD1=
,BD1=
,
∴AB与DB1所成的角为90°,故⑤不正确.
故答案为:①②④.
∴AC⊥平BDB1,∴DB1⊥AC,
同理,DB1⊥D1C,∴DB1⊥平面ACD1,故①正确;
对于②,∵AD1∥BC1,
AD1不包含于平面ACD1,BC1?平面ACD1,
∴AD1∥平面BCC1,故②正确;
对于③,∵AD与DB的夹角为45°,DB?平面D1DB,
∴AD与平面D1DB一定不垂直,故③不正确;
对于④,∵DB1⊥平面ACD1,DB1?B1D1D,
∴平面ACD1⊥平面B1D1D,故④正确;
对于⑤,设AB=a,则AD1=
| 2 |
| 3 |
∴AB与DB1所成的角为90°,故⑤不正确.
故答案为:①②④.
点评:本题考查直线与平面、平面与平南的位置关系的判断,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
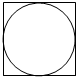 在图的正方形中随机撒一把芝麻,用随机模拟的方法估计圆周率π的值.如果撒了1000个芝麻,落在圆内的芝麻总数是781颗,那么这次模拟中π的估计值是
在图的正方形中随机撒一把芝麻,用随机模拟的方法估计圆周率π的值.如果撒了1000个芝麻,落在圆内的芝麻总数是781颗,那么这次模拟中π的估计值是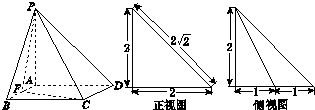 如图所示,在四棱锥P-ABCD中,PA⊥底面ABCD,四边形ABCD为正方形,F为AB上一点.该四棱锥的正视图和侧视图如图所示,则四面体P-BFC的体积是
如图所示,在四棱锥P-ABCD中,PA⊥底面ABCD,四边形ABCD为正方形,F为AB上一点.该四棱锥的正视图和侧视图如图所示,则四面体P-BFC的体积是