题目内容
已知⊙C:x2+y2=r2(r>0)在点P(x0,y0)处的切线方程为x0x+y0y=r2.请类比此结论,在椭圆中也有类似结论:在椭圆
+
=1(a>b>0)上一点Q(x1,y1)处的切线方程为 .
| x2 |
| a2 |
| y2 |
| b2 |
考点:类比推理
专题:推理和证明
分析:由过圆x2+y2=r2上一点的切线方程x0x+y0y=r2,我们不难类比推断出过椭圆上一点的切线方程:用x0x代x2,用y0y代y2,即可得.
解答:
解:类比过圆上一点的切线方程,可合情推理:
过椭圆
+
=1(a>b>0)上一点Q(x1,y1)处的切线方程为
+
=1(a>b>0).
故答案为:
+
=1(a>b>0).
过椭圆
| x2 |
| a2 |
| y2 |
| b2 |
| x1x |
| a2 |
| y1y |
| b2 |
故答案为:
| x1x |
| a2 |
| y1y |
| b2 |
点评:本题考查利用类比推理得到结论、证明类比结论时证明过程与其类比对象的证明过程类似或直接转化为类比对象的结论.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
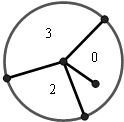 如图所示,旋转一次的圆盘,指针落在圆盘中3分处的概率为a,落在圆盘中2分处的概率为b,落在圆盘中0分处的概率为c,(a,b,c∈(0,1)),已知旋转一次圆盘得分的数学期望为1分,则
如图所示,旋转一次的圆盘,指针落在圆盘中3分处的概率为a,落在圆盘中2分处的概率为b,落在圆盘中0分处的概率为c,(a,b,c∈(0,1)),已知旋转一次圆盘得分的数学期望为1分,则| 2 |
| a |
| 1 |
| 3b |
A、
| ||
B、
| ||
C、
| ||
D、
|
将正方形ABCD沿对角线BD折成一个直二面角,点C到达点C1,则异面直线AB与C1D所成角是( )
| A、90° | B、60° |
| C、45° | D、30° |
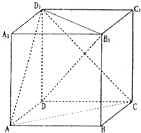 在正方体ABCD-A1B1C1D1中,给出以下结论:
在正方体ABCD-A1B1C1D1中,给出以下结论: