题目内容
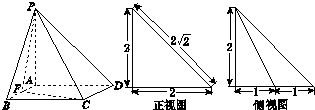 如图所示,在四棱锥P-ABCD中,PA⊥底面ABCD,四边形ABCD为正方形,F为AB上一点.该四棱锥的正视图和侧视图如图所示,则四面体P-BFC的体积是
如图所示,在四棱锥P-ABCD中,PA⊥底面ABCD,四边形ABCD为正方形,F为AB上一点.该四棱锥的正视图和侧视图如图所示,则四面体P-BFC的体积是考点:二面角的平面角及求法
专题:空间位置关系与距离
分析:利用左视图可得 F为AB的中点,即可得到三角形BFC的面积,由PA⊥平面ABCD,可知PA是四面体PBFC的底面BFC上的高,利用三棱锥的体积计算公式即可得到;
解答:
解:由侧视图可得 F为AB的中点,
∴△BFC的面积为S=
×1×2=1.
∵PA⊥平面ABCD,
∴四面体P-BFC的体积V=
S△BFC•PA=
×1×2=
.
故答案为:
∴△BFC的面积为S=
| 1 |
| 2 |
∵PA⊥平面ABCD,
∴四面体P-BFC的体积V=
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
故答案为:
| 2 |
| 3 |
点评:本题主要考查棱锥的体积计算,正确理解三视图,熟练掌握三角形BFC的面积、三棱锥的体积计算公式是解题的关键.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
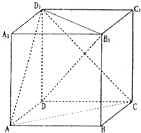 在正方体ABCD-A1B1C1D1中,给出以下结论:
在正方体ABCD-A1B1C1D1中,给出以下结论: