题目内容
计算
-cos585°•tan（-
π）．
| ||
tan
|
| 37 |
| 4 |
考点：同角三角函数基本关系的运用,运用诱导公式化简求值
专题：三角函数的求值
分析：原式中的角度变形后，利用诱导公式化简，再利用特殊角的三角函数值计算即可得到结果．
解答：
解：原式=
+cos225°tan
=
-cos45°tan
=
-
=
．
-
| ||
tan
|
| π |
| 4 |
=
-
| ||
-tan
|
| π |
| 4 |
=
| ||||||
|
| ||
| 2 |
=
| ||||
| 2 |
点评：此题考查了同角三角函数基本关系的运用，熟练掌握基本关系是解本题的关键．
练习册系列答案
相关题目
下列函数中与y=cosx奇偶性相同的是（ ）
| A、y=tanx |
| B、y=|sinx| |
| C、y=sinx |
| D、y=-sinx |
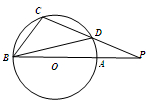如图，AB是半径为3的⊙O的直径，CD是弦，BA，CD的延长线交于点P，PA=4，PD=5，则∠CBD=
如图，在△ABC中，AD是的∠A的平分线，圆O经过点A与BC切于点D，与AB，AC相交于E、F，连结DF，DE．