题目内容
 如图,在△ABC中,AD是的∠A的平分线,圆O经过点A与BC切于点D,与AB,AC相交于E、F,连结DF,DE.
如图,在△ABC中,AD是的∠A的平分线,圆O经过点A与BC切于点D,与AB,AC相交于E、F,连结DF,DE.(Ⅰ)求证:EF∥BC;
(Ⅱ)求证:DF2=AF•BE.
考点:与圆有关的比例线段,圆的切线的判定定理的证明
专题:选作题,立体几何
分析:(Ⅰ)证明EF∥BC,只需证明∠FDC=∠EFD,利用圆的切线的性质可得;
(Ⅱ)证明DF2=AF•BE,只需证明△AFD∽△DEB.
(Ⅱ)证明DF2=AF•BE,只需证明△AFD∽△DEB.
解答:
证明:(Ⅰ)因为BC是圆O的切线,所以∠FDC=∠FAD,
又因为∠EAD=∠EFD,且∠EAD=∠FAD,
所以∠FDC=∠EFD,
所以EF∥BC.-----------(5分)
(Ⅱ) 连接ED,△AFD,△DEB中,∠EDB=∠EAD=∠FAD,∠BED=∠DFA,
所以△AFD∽△DEB,
所以
=
,
又因为DE=DF,
所以DF2=AF•BE.-----------(10分)
又因为∠EAD=∠EFD,且∠EAD=∠FAD,
所以∠FDC=∠EFD,
所以EF∥BC.-----------(5分)
(Ⅱ) 连接ED,△AFD,△DEB中,∠EDB=∠EAD=∠FAD,∠BED=∠DFA,
所以△AFD∽△DEB,
所以
| AF |
| DE |
| FD |
| EB |
又因为DE=DF,
所以DF2=AF•BE.-----------(10分)
点评:本题考查三角形的相似,考查圆的切线性质,考查学生分析解决问题的能力,正确判断三角形相似是关键.

练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目
直线3x-4y-9=0与圆x2+y2=4的位置关系是( )
| A、相交但不过圆心 | B、相交且过圆心 |
| C、相切 | D、相离 |
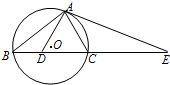 已知圆O的内接△ABC中,D为BC上一点,且△ADC为正三角形,点E为BC的延长线上一点,AE为圆O的切线,求证:CD2=BD•EC.
已知圆O的内接△ABC中,D为BC上一点,且△ADC为正三角形,点E为BC的延长线上一点,AE为圆O的切线,求证:CD2=BD•EC.