题目内容
已知函数f(x)=
ax2-(2a+1)x+2lnx(x∈R).
(1)若曲线y=f(x)在x=1和x=3处的切线互相平行,求a的值及函数y=f(x)的单调区间;
(2)设g(x)=(x2-2x)ex,若对任意x1∈(0,2),均存在x2∈(0,2),使得f(x1)<g(x2),求实数a的取值范围.
| 1 |
| 2 |
(1)若曲线y=f(x)在x=1和x=3处的切线互相平行,求a的值及函数y=f(x)的单调区间;
(2)设g(x)=(x2-2x)ex,若对任意x1∈(0,2),均存在x2∈(0,2),使得f(x1)<g(x2),求实数a的取值范围.
考点:导数在最大值、最小值问题中的应用
专题:导数的综合应用
分析:(1)由导数的几何意义,根据曲线y=f(x)在x=l和x=3处的切线互相平行,求得a值,再利用导数求得单调区间;
(2)由题意得,若要命题成立,只须当x∈[0,2]时,f(x)max<g(x)max.利用导数分别求得f(x)、g(x)的最大值,解不等式得出a的取值范围.
(2)由题意得,若要命题成立,只须当x∈[0,2]时,f(x)max<g(x)max.利用导数分别求得f(x)、g(x)的最大值,解不等式得出a的取值范围.
解答:
解:(1)∵f(x)=
ax2-(2a+1)x+2lnx(x∈R).
∴f′(x)=ax-(2a+1)+
,f′(1)=-a+1,f′(3)=a-
,
由f′(1)=f′(3)得a=
,f′(x)=
x-
+
,----------------------(3分)
所以y=f(x)的单调递增区间为(0,
),(2,+∞),
单调递减区间为(
,2)-------------------------------(6分)
(2)若要命题成立,只须当x∈[0,2]时,f(x)max<g(x)max.
由g'(x)=(x2-2)ex可知,当x∈(0,2]时g(x)max=g(2)=0,
所以只须f(x)max<0.-----------------------------------(8分)
对f(x)来说,f′(x)=ax-(2a+1)+
=
,
①当a>
时,f(x)max=f(
)=-2lna-
-2,
当a≥1时,显然f(x)max<0,满足题意,
当
<a<1时,令h(x)=-2lnx-
-2(
<x<1),h′(x)=-
+
<0,所以h(x)递减,所以h(x)<0,满足题意,
所以a>
满足题意;-----------------------------(10分)
②当a≤
时,f(x)在x∈(0,2)上单调递增,
所以f(x)max=f(2)=2ln2-2a-2<0得ln2-1<a≤
,…(12分)
综上所述,a>ln2-1.---------------------------(13分)
| 1 |
| 2 |
∴f′(x)=ax-(2a+1)+
| 2 |
| x |
| 1 |
| 3 |
由f′(1)=f′(3)得a=
| 2 |
| 3 |
| 2 |
| 3 |
| 7 |
| 3 |
| 2 |
| x |
所以y=f(x)的单调递增区间为(0,
| 3 |
| 2 |
单调递减区间为(
| 3 |
| 2 |
(2)若要命题成立,只须当x∈[0,2]时,f(x)max<g(x)max.
由g'(x)=(x2-2)ex可知,当x∈(0,2]时g(x)max=g(2)=0,
所以只须f(x)max<0.-----------------------------------(8分)
对f(x)来说,f′(x)=ax-(2a+1)+
| 2 |
| x |
| (ax-1)(x-2) |
| x |
①当a>
| 1 |
| 2 |
| 1 |
| a |
| 1 |
| 2a |
当a≥1时,显然f(x)max<0,满足题意,
当
| 1 |
| 2 |
| 1 |
| 2x |
| 1 |
| 2 |
| 2 |
| x |
| 1 |
| 2x2 |
所以a>
| 1 |
| 2 |
②当a≤
| 1 |
| 2 |
所以f(x)max=f(2)=2ln2-2a-2<0得ln2-1<a≤
| 1 |
| 2 |
综上所述,a>ln2-1.---------------------------(13分)
点评:本题主要考查利用导数求曲线的切线斜率及利用导数研究函数的单调性、最值等知识,考查等价转化思想、分类讨论思想等运用能力,属难题.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
设复数Z满足Zi=2-i,则|Z|=( )
A、
| ||
B、
| ||
C、
| ||
| D、3 |
 某市为调研学校师生的环境保护意识,决定在本市所有学校中随机抽取60所进行环境综合考评成绩达到80分以上(含80分)为达标.60所学校的考评结果频率分布直方图如图所示(其分组区间为[50,60),[60,70),[70,80),[80,90),[90,100]).
某市为调研学校师生的环境保护意识,决定在本市所有学校中随机抽取60所进行环境综合考评成绩达到80分以上(含80分)为达标.60所学校的考评结果频率分布直方图如图所示(其分组区间为[50,60),[60,70),[70,80),[80,90),[90,100]).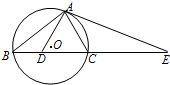 已知圆O的内接△ABC中,D为BC上一点,且△ADC为正三角形,点E为BC的延长线上一点,AE为圆O的切线,求证:CD2=BD•EC.
已知圆O的内接△ABC中,D为BC上一点,且△ADC为正三角形,点E为BC的延长线上一点,AE为圆O的切线,求证:CD2=BD•EC.