题目内容
7.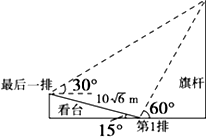 某校运动会开幕式上举行升旗仪式,在坡度为15°的看台上,同一列上的第一排和最后一排测得旗杆顶部的仰角分别为60°和30°,第一排和最后一排的距离为$10\sqrt{6}$m(如图所示),则旗杆的高度为( )
某校运动会开幕式上举行升旗仪式,在坡度为15°的看台上,同一列上的第一排和最后一排测得旗杆顶部的仰角分别为60°和30°,第一排和最后一排的距离为$10\sqrt{6}$m(如图所示),则旗杆的高度为( )| A. | 10m | B. | 30m | C. | 10m | D. | 10m |
分析 作图,分别求得∠ABC,∠ACB和∠BAC,然后利用正弦定理求得AC,最后在直角三角形ACD中求得AD.
解答 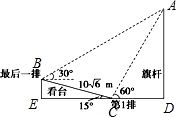 解:如图,
解:如图,
依题意知∠ABC=30°+15°=45°,∠ACB=180°-60°-15°=105°,
∴∠BAC=180°-45°-105°=30°,
由正弦定理知AC=$\frac{BC}{sin∠BAC}$•sin∠ABC=20$\sqrt{3}$(m),
在Rt△ACD中,AD=$\frac{\sqrt{3}}{2}$•AC=$\frac{\sqrt{3}}{2}$×20$\sqrt{3}$=30(m),
即旗杆的高度为30m.
故选B.
点评 本题主要考查了解三角形的实际应用.结合了正弦定理等基础知识,考查了学生分析和推理的能力,属于中档题.

练习册系列答案
相关题目
18.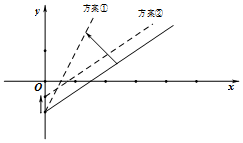 如图是某条公共汽车线路收支差额y与乘客量x的图象(实线),由于目前本线路亏损,公司有关人员提出两种扭亏为盈的方案(虚线),这两种方案分别是( )
如图是某条公共汽车线路收支差额y与乘客量x的图象(实线),由于目前本线路亏损,公司有关人员提出两种扭亏为盈的方案(虚线),这两种方案分别是( )
 如图是某条公共汽车线路收支差额y与乘客量x的图象(实线),由于目前本线路亏损,公司有关人员提出两种扭亏为盈的方案(虚线),这两种方案分别是( )
如图是某条公共汽车线路收支差额y与乘客量x的图象(实线),由于目前本线路亏损,公司有关人员提出两种扭亏为盈的方案(虚线),这两种方案分别是( )| A. | 方案①降低成本,票价不变,方案②提高票价而成本不变; | |
| B. | 方案①提高票价而成本不变,方案②降低成本,票价不变; | |
| C. | 方案①降低成本,票价提高,方案②提高票价而成本不变; | |
| D. | 方案①提高成本,票价不变,方案②降低票价且成本降低 |
15.已知a,b,c分别为△ABC三个内角A,B,C的对边,(sinA+sinB)(a-b)=(sinC-sinB)c,S△ABC=$\sqrt{3}$,c=4b,则函数f(x)=bx2-ax+c的零点个数为( )
| A. | 0 | B. | 1 | C. | 2 | D. | 不确定 |
16.已知集合A={x|x2-2x-3≥0},B={x|y=log2(x-1)},则(∁RA)∩B=( )
| A. | (1,3) | B. | (-1,3) | C. | (3,5) | D. | (-1,5) |
17.命题“?x∈R,sinx>0”的否定是( )
| A. | ?x∈R,sinx<0 | B. | ?x∈R,sinx≤0 | C. | ?x∈R,sinx≤0 | D. | ?x∈R,sinx<0 |