题目内容
15.已知a,b,c分别为△ABC三个内角A,B,C的对边,(sinA+sinB)(a-b)=(sinC-sinB)c,S△ABC=$\sqrt{3}$,c=4b,则函数f(x)=bx2-ax+c的零点个数为( )| A. | 0 | B. | 1 | C. | 2 | D. | 不确定 |
分析 利用余弦定理,结合三角形的面积,求出a,b,c,然后求解函数零点个数.
解答 解:a,b,c分别为△ABC三个内角A,B,C的对边,
(sinA+sinB)(a-b)=(sinC-sinB)c,
由正弦定理可得,(a+b)(a-b)=(c-b)c,可得a2=b2+c2-bc,
可得cosA=$\frac{1}{2}$,sinA=$\frac{\sqrt{3}}{2}$,S△ABC=$\sqrt{3}$,$\sqrt{3}$=$\frac{1}{2}bcsinA$,可得bc=4,又c=4b,
解得c=4,b=1,则a=$\sqrt{13}$.
函数f(x)=bx2-ax+c=x2-$\sqrt{13}$x+4,函数的开口向上,
△=13-16=-3<0,二次函数与x轴没有交点,
所以函数的零点个数为0.
点评 此题考查了正弦、余弦定理的应用,二次函数的简单性质的应用,函数零点的求法,熟练掌握定理是解本题的关键.

练习册系列答案
相关题目
6.复数$\frac{1+2i}{2-i}$化简是( )
| A. | $\frac{3i}{5}$ | B. | $-\frac{3i}{5}$ | C. | i | D. | -i |
10.命题“对任意x∈R,都有x2≥0”的否定为( )
| A. | 对任意x∈R,使得x2<0 | B. | 不存在x∈R,使得x2<0 | ||
| C. | 存在x0∈R,都有$x_0^2≥0$ | D. | 存在x0∈R,都有$x_0^2<0$ |
7.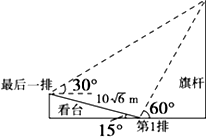 某校运动会开幕式上举行升旗仪式,在坡度为15°的看台上,同一列上的第一排和最后一排测得旗杆顶部的仰角分别为60°和30°,第一排和最后一排的距离为$10\sqrt{6}$m(如图所示),则旗杆的高度为( )
某校运动会开幕式上举行升旗仪式,在坡度为15°的看台上,同一列上的第一排和最后一排测得旗杆顶部的仰角分别为60°和30°,第一排和最后一排的距离为$10\sqrt{6}$m(如图所示),则旗杆的高度为( )
 某校运动会开幕式上举行升旗仪式,在坡度为15°的看台上,同一列上的第一排和最后一排测得旗杆顶部的仰角分别为60°和30°,第一排和最后一排的距离为$10\sqrt{6}$m(如图所示),则旗杆的高度为( )
某校运动会开幕式上举行升旗仪式,在坡度为15°的看台上,同一列上的第一排和最后一排测得旗杆顶部的仰角分别为60°和30°,第一排和最后一排的距离为$10\sqrt{6}$m(如图所示),则旗杆的高度为( )| A. | 10m | B. | 30m | C. | 10m | D. | 10m |
5.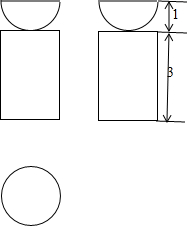 如图是一个组合体的三视图,根据图中数据,可得该几何体的体积是( )
如图是一个组合体的三视图,根据图中数据,可得该几何体的体积是( )
 如图是一个组合体的三视图,根据图中数据,可得该几何体的体积是( )
如图是一个组合体的三视图,根据图中数据,可得该几何体的体积是( )| A. | $\frac{38π}{3}$ | B. | $\frac{19π}{3}$ | C. | $\frac{13π}{3}$ | D. | $\frac{11π}{3}$ |
