题目内容
已知p:-2≤1-
≤2,q:x2-2x+1-m2≤0(m>0).若“非p”是“非q”的充分而不必要条件,求实数m的取值范围.
| x-1 |
| 3 |
考点:复合命题的真假
专题:简易逻辑
分析:先解出p,q下的不等式,再求出非p,非q,根据非p是非q的充分不必要条件即可得到限制m的不等式,解不等式即得m的取值范围.
解答:
解:解-2≤1-
≤2得:-2≤x≤10,解x2-2x+1-m2≤0得:1-m≤x≤1+m;
∴非p:x<-2,或x>10;
非q:x<1-m,或x>1+m;
∵“非p”是“非q”的充分而不必要条件,即由非p能得到非q,而由非q得不到非p;
∴1-m≥-2,且1+m≤10,解得m≤3;
∴实数m的取值范围为(-∞,3].
| x-1 |
| 3 |
∴非p:x<-2,或x>10;
非q:x<1-m,或x>1+m;
∵“非p”是“非q”的充分而不必要条件,即由非p能得到非q,而由非q得不到非p;
∴1-m≥-2,且1+m≤10,解得m≤3;
∴实数m的取值范围为(-∞,3].
点评:考查分式不等式,一元二次不等式的求解,充分条件的概念,必要条件的概念,充分不必要条件的概念,本题也可借助数轴求解.

练习册系列答案
 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
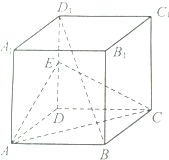 如图,正方体ABCD-A1B1C1D1中,E为DD1的中点.
如图,正方体ABCD-A1B1C1D1中,E为DD1的中点.