题目内容
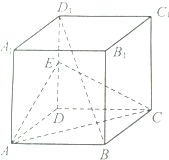 如图,正方体ABCD-A1B1C1D1中,E为DD1的中点.
如图,正方体ABCD-A1B1C1D1中,E为DD1的中点.(Ⅰ)证明:AC⊥BD1;
(Ⅱ)证明:BD1∥平面ACE.
考点:直线与平面垂直的性质,直线与平面平行的判定
专题:证明题,空间位置关系与距离
分析:(I)证明AC⊥BD,且AC⊥DD1,即可证明AC⊥平面BDD1,从而证明AC⊥BD1;
( II)如图所示,证明OE∥BD1,即可证明BD1∥平面ACE.
( II)如图所示,证明OE∥BD1,即可证明BD1∥平面ACE.
解答:
解:(I)证明:在正方体ABCD中,连结BD,
∴AC⊥BD,
又∵DD1⊥平面ABCD,且AC?平面ABCD,
∴AC⊥DD1,
又BD∩DD1=D,
∴AC⊥平面BDD1;
又∵BD1?平面BDD1,
∴AC⊥BD1;如图所示;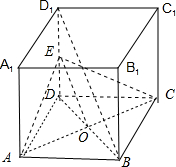
( II)证明:设BD∩AC=O,连结OE,
在△BDD1中,O、E分别为BD、DD1的中点,
∴OE∥BD1;
又∵OE?平面ACE,且BD1?平面ACE,
∴BD1∥平面ACE.
∴AC⊥BD,
又∵DD1⊥平面ABCD,且AC?平面ABCD,
∴AC⊥DD1,
又BD∩DD1=D,
∴AC⊥平面BDD1;
又∵BD1?平面BDD1,
∴AC⊥BD1;如图所示;

( II)证明:设BD∩AC=O,连结OE,
在△BDD1中,O、E分别为BD、DD1的中点,
∴OE∥BD1;
又∵OE?平面ACE,且BD1?平面ACE,
∴BD1∥平面ACE.
点评:本题考查了空间中的垂直与平行关系的证明问题,解题时应结合图形,弄清空间中的平行与垂直的条件与结论是什么,是中档题目.

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
cos2
-sin2
=( )
| π |
| 12 |
| π |
| 12 |
A、
| ||||
B、-
| ||||
C、-
| ||||
D、
|
 如图,已知AB是平面α的一条斜线,B为斜足,AO⊥α,O为垂足,BC为α内的一条直线,∠ABC=60°,∠OBC=45°,求斜线AB和平面α所成角.
如图,已知AB是平面α的一条斜线,B为斜足,AO⊥α,O为垂足,BC为α内的一条直线,∠ABC=60°,∠OBC=45°,求斜线AB和平面α所成角.