题目内容
若将函数f(x)=sinx+cosx的图象向右平移P个单位,所得图象关于原点对称,则P的最小正值是 .
考点:函数y=Asin(ωx+φ)的图象变换
专题:计算题,三角函数的图像与性质
分析:根据辅助角公式,化简函数得y=
sin(x+
),从而得出平移后的图象对应的函数为y=
sin(x+
-P).由平移后的图象关于原点对称,根据正弦函数的图象与性质得到∴
-P=kπ(k∈Z),再取k=0得到P的最小正值.
| 2 |
| π |
| 4 |
| 2 |
| π |
| 4 |
| π |
| 4 |
解答:
解:y=sinx+cosx=
(sinxcos
+cosxsin
)=
sin(x+
).
将函数的图象向右平移P个单位长度后,得到y=
sin[(x-P)+
]=
sin(x+
-P)的图象.
∵平移后得到的图象关于坐标原点对称,
∴
-P=kπ(k∈Z),可得P=
-kπ(k∈Z),
取k=0,得到P的最小正值为
.
故答案为:
.
| 2 |
| π |
| 4 |
| π |
| 4 |
| 2 |
| π |
| 4 |
将函数的图象向右平移P个单位长度后,得到y=
| 2 |
| π |
| 4 |
| 2 |
| π |
| 4 |
∵平移后得到的图象关于坐标原点对称,
∴
| π |
| 4 |
| π |
| 4 |
取k=0,得到P的最小正值为
| π |
| 4 |
故答案为:
| π |
| 4 |
点评:本题给出三角函数表达式,已知函数图象右移P个单位个图象关于原点对称,求平移的最小长度.着重考查了三角恒等变换公式、正弦函数的图象与性质和函数图象平移公式等知识,属于中档题.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目

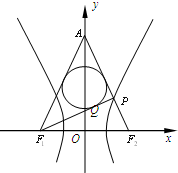 如图,已知双曲线
如图,已知双曲线