题目内容
现有4个同学去看电影,他们坐在了同一排,且一排有6个座位.问:
(1)所有可能的坐法有多少种?
(2)此4人中甲,乙两人相邻的坐法有多少种?
(3)所有空位不相邻的坐法有多少种?(结果均用数字作答)
(1)所有可能的坐法有多少种?
(2)此4人中甲,乙两人相邻的坐法有多少种?
(3)所有空位不相邻的坐法有多少种?(结果均用数字作答)
考点:排列、组合及简单计数问题
专题:排列组合
分析:(1)4个同学去看电影,他们坐在了同一排,且一排有6个座位,所有可能的坐法种数是从六个元素中取四个元素的排列数,由此能求出所有可能的坐法种数.
(2)4人中甲,乙两人相邻,用捆绑法能得到4人中甲,乙两人相邻的坐法种数.
(3)所有空位不相邻用插空法,先把4人排成一排,有
种排法,再往4个人构成的个空中插入两个空座位,有
种插入方法,由乘法原理,能得到所有空位不相邻的坐法种数.
(2)4人中甲,乙两人相邻,用捆绑法能得到4人中甲,乙两人相邻的坐法种数.
(3)所有空位不相邻用插空法,先把4人排成一排,有
| A | 4 4 |
| C | 2 5 |
解答:
解:(1)4个同学去看电影,他们坐在了同一排,且一排有6个座位,
所有可能的坐法种数是从六个元素中取四个元素的排列数,
∴所有可能的坐法有
=360种.
(2)4人中甲,乙两人相邻,用捆绑法得到4人中甲,乙两人相邻的坐法有
=120种.…8分
(3)所有空位不相邻用插空法,先把4人排成一排,有
种排法,
再往4个人构成的个空中插入两个空座位,有
种插入方法,
由乘法原理,得所有空位不相邻的坐法有
=240种.
所有可能的坐法种数是从六个元素中取四个元素的排列数,
∴所有可能的坐法有
| A | 4 6 |
(2)4人中甲,乙两人相邻,用捆绑法得到4人中甲,乙两人相邻的坐法有
| A | 2 2 |
| A | 3 5 |
(3)所有空位不相邻用插空法,先把4人排成一排,有
| A | 4 4 |
再往4个人构成的个空中插入两个空座位,有
| C | 2 5 |
由乘法原理,得所有空位不相邻的坐法有
| A | 4 4 |
| C | 2 5 |
点评:本题考查排列组合中元素相邻问题、不相邻问题的处理方法,即采用捆绑法、插空法和计数原理,分类计数问题是经常出现的一个问题,解题时一定要分清做这件事需要分为几类,每一类包含几种方法,把几个步骤中数字相加得到结果.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
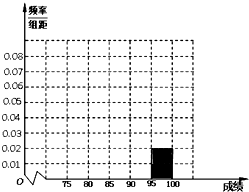 某校高三年级在高校自主招生期间,把学生的平时成绩按“百分制”折算并排序,选出前300名学生,并对这300名学生按成绩分组,第一组[75,80),第二组[80,85),第三组[85,90),第四组[90,95),第五组[95,100],如图为频率分布直方图的一部分,其中第五组、第一组、第四组、第二组、第三组的人数依次成等差数列.
某校高三年级在高校自主招生期间,把学生的平时成绩按“百分制”折算并排序,选出前300名学生,并对这300名学生按成绩分组,第一组[75,80),第二组[80,85),第三组[85,90),第四组[90,95),第五组[95,100],如图为频率分布直方图的一部分,其中第五组、第一组、第四组、第二组、第三组的人数依次成等差数列.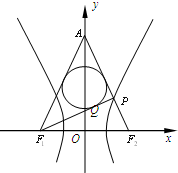 如图,已知双曲线
如图,已知双曲线