题目内容
已知函数f(x)=|x+1|+|x-a|
(Ⅰ)若a=3,解不等式f(x)≥6;
(Ⅱ)若不等式f(x)≥6对任意的实数x恒成立,求实数a的取值范围.
(Ⅰ)若a=3,解不等式f(x)≥6;
(Ⅱ)若不等式f(x)≥6对任意的实数x恒成立,求实数a的取值范围.
考点:绝对值不等式的解法
专题:不等式的解法及应用
分析:(Ⅰ)若a=3,不等式即|x+1|+|x-3|≥6,根据绝对值的意义求得|x+1|+|x-3|≥6的解集.
(Ⅱ)根据绝对值的意义,|x+1|+|x-a|的最小值为|a+1|,由|a+1|≥6,求得实数a的取值范围.
(Ⅱ)根据绝对值的意义,|x+1|+|x-a|的最小值为|a+1|,由|a+1|≥6,求得实数a的取值范围.
解答:
解:(Ⅰ)若a=3,不等式f(x)≥6,即|x+1|+|x-3|≥6.
根据绝对值的意义,|x+1|+|x-3|表示数轴上的x对应点到-1、3对应点的距离之和,
而数轴上-2 和4对应点满足对应点到-1、3对应点的距离之和正好等于6,
故|x+1|+|x-3|≥6的解集为(-∞,-2]∪[4,+∞).
(Ⅱ)根据绝对值的意义,|x+1|+|x-a|表示数轴上的x对应点到-1、a对应点的距离之和,
它的最小值为|a+1|,
若不等式f(x)≥6对任意的实数x恒成立,则|a+1|≥6,求得a≥5,或a≤-7,
故实数a的取值范围为(-∞,-7]∪[5,+∞).
根据绝对值的意义,|x+1|+|x-3|表示数轴上的x对应点到-1、3对应点的距离之和,
而数轴上-2 和4对应点满足对应点到-1、3对应点的距离之和正好等于6,
故|x+1|+|x-3|≥6的解集为(-∞,-2]∪[4,+∞).
(Ⅱ)根据绝对值的意义,|x+1|+|x-a|表示数轴上的x对应点到-1、a对应点的距离之和,
它的最小值为|a+1|,
若不等式f(x)≥6对任意的实数x恒成立,则|a+1|≥6,求得a≥5,或a≤-7,
故实数a的取值范围为(-∞,-7]∪[5,+∞).
点评:本题主要考查绝对值的意义,绝对值不等式的解法,函数的恒成立问题,体现了转化的数学思想,属于基础题.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案
相关题目
若函数f(x)=x3-ax2+4在(0,2)内单调递减,则实数a的取值范围为( )
| A、[3,+∞) |
| B、{3} |
| C、(-∞,3] |
| D、(0,3) |
 已知圆O:x2+y2=4,直线l:kx-y-k-1=0
已知圆O:x2+y2=4,直线l:kx-y-k-1=0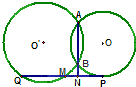 如图,⊙O′和⊙O相交于A和B,PQ切⊙O于P,交⊙O′于Q和M,交AB的延长线于N,MN=3,NQ=15,求PN的长.
如图,⊙O′和⊙O相交于A和B,PQ切⊙O于P,交⊙O′于Q和M,交AB的延长线于N,MN=3,NQ=15,求PN的长.