题目内容
 已知圆O:x2+y2=4,直线l:kx-y-k-1=0
已知圆O:x2+y2=4,直线l:kx-y-k-1=0(1)判断直线l和圆O的位置关系.
(2)求圆心到直线l的距离的最大值.
(3)如图所示,圆O与y轴的正方向交于A点,点B在直线y=2上运动,过B做圆O的切线,切点为C,求△ABC垂心H的轨迹.
考点:直线和圆的方程的应用
专题:直线与圆
分析:(1)判断直线l过定点(1,1),根据点与圆的关系,即可判断直线l和圆O的位置关系.
(2)根据圆心到直线的距离公式即可求圆心到直线l的距离的最大值.
(3)设垂心的坐标,根据条件,建立方程关系,即可求出H的轨迹方程.
(2)根据圆心到直线的距离公式即可求圆心到直线l的距离的最大值.
(3)设垂心的坐标,根据条件,建立方程关系,即可求出H的轨迹方程.
解答:
解:(1)∵kx-y-k-1=0
∴y=k(x-1)-1
∴直线l经过定点P(1,-1),
又∵(1,-1)在圆的内部
∴直线l与圆O相交.
(2)由(1)知圆心到直线l的最大距离为|OP|=
.
(3)设H(x,y),C(x′,y′),连结AH,CH,
则AH⊥BC,CH⊥AB,BC是切线OC⊥BC,
∴OC∥AH,CH∥OA,OA=OC,
∴四边形AOCH是菱形.
∴|CH|=|OA|=2,得
,
又C(x′,y′),满足x′2+y′2=4,
所以x2+(y-2)2=4,(x≠0)即是所求轨迹方程.
∴y=k(x-1)-1
∴直线l经过定点P(1,-1),
又∵(1,-1)在圆的内部
∴直线l与圆O相交.
(2)由(1)知圆心到直线l的最大距离为|OP|=
| 2 |
(3)设H(x,y),C(x′,y′),连结AH,CH,
则AH⊥BC,CH⊥AB,BC是切线OC⊥BC,
∴OC∥AH,CH∥OA,OA=OC,
∴四边形AOCH是菱形.
∴|CH|=|OA|=2,得
|
又C(x′,y′),满足x′2+y′2=4,
所以x2+(y-2)2=4,(x≠0)即是所求轨迹方程.
点评:本题主要考查直线和圆的位置关系的判断和应用,以及轨迹的求解吗,考查学生的计算能力.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
在极坐标系中,圆ρ=2sinθ的圆心到极轴的距离为( )
| A、1 | ||
B、
| ||
C、
| ||
| D、2 |
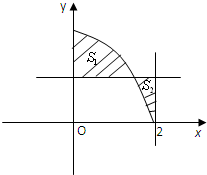 如图,已知S1为直线x=0,y=4-t2及y=4-x2所围成的面积,S2为直线x=2,y=4-t2及y=4-x2所围成图形的面积(t为常数).
如图,已知S1为直线x=0,y=4-t2及y=4-x2所围成的面积,S2为直线x=2,y=4-t2及y=4-x2所围成图形的面积(t为常数).