题目内容
已知数列{an}的前n项和为Sn=3n-1，那么该数列的通项公式为an= ．
考点：数列递推式
专题：计算题,等差数列与等比数列
分析：由Sn=3n-1，得Sn-1=3n-1-1（n≥2），两式相减可得an，注意讨论n=1时的情形．
解答：
解：由Sn=3n-1①，得Sn-1=3n-1-1（n≥2）②，
①-②，得an=2×3n-1（n≥2），
当n=1时，a1=S1=2，适合上式，
∴an=2×3n-1．
故答案为：2×3n-1．
①-②，得an=2×3n-1（n≥2），
当n=1时，a1=S1=2，适合上式，
∴an=2×3n-1．
故答案为：2×3n-1．
点评：该题考查数列递推式，考查an与Sn的关系：an=
．
|
练习册系列答案
相关题目
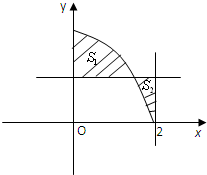如图，已知S1为直线x=0，y=4-t2及y=4-x2所围成的面积，S2为直线x=2，y=4-t2及y=4-x2所围成图形的面积（t为常数）．