题目内容
已知数列{an}的前n项和为Sn,且a1=3,an+1-an=2,则
的最小值为 .
| Sn+33 |
| n |
考点:等差数列的前n项和,数列的函数特性
专题:等差数列与等比数列
分析:利用等差数列的前n项和公式求出Sn+33,再利用均值定理能求出
的最小值.
| Sn+33 |
| n |
解答:
解:由题意知数列{an}是首项a1=3,公差d=2的等差数列,
∴Sn=3n+
×2=n2+2n,
∴
=
=n+
+2
≥2
+2
=2
+2,
∵5<
<6,n∈N*,
∴
的最小值为12.
故答案为:12.
∴Sn=3n+
| n(n-1) |
| 2 |
∴
| Sn+33 |
| n |
| n2+2n+33 |
| n |
=n+
| 33 |
| n |
≥2
n•
|
=2
| 33 |
∵5<
| 33 |
∴
| Sn+33 |
| n |
故答案为:12.
点评:本题考查最小值的求法,是中档题,解题时要认真审题,注意均值定理的合理运用.

练习册系列答案
相关题目
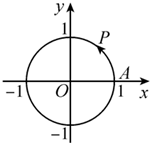 如图,半径为1的圆的圆心位于坐标原点,点P从点A(1,0)出发,依逆时针方向等速沿单位圆周旋转.已知点P在1秒钟内转过的角度为θ(0<θ<π),经过2秒钟到达第三象限,经过14秒钟后又恰好回到出发点A,则θ=
如图,半径为1的圆的圆心位于坐标原点,点P从点A(1,0)出发,依逆时针方向等速沿单位圆周旋转.已知点P在1秒钟内转过的角度为θ(0<θ<π),经过2秒钟到达第三象限,经过14秒钟后又恰好回到出发点A,则θ=