题目内容
已知直线l1:ax+2y+6=0,直线l2:x+(a-1)y+a2-1=0.当a 时,l1与l2相交;当a 时,l1⊥l2;当a 时,l1与l2重合;当a 时,l1∥l2.
考点:方程组解的个数与两直线的位置关系
专题:直线与圆
分析:由a(a-1)-2×1=0可解得a=-1或a=2,验证可得两直线平行,重合,相交的条件,由a×1+2(a-1)=0可解得垂直的条件.
解答:
解:由a(a-1)-2×1=0可解得a=-1或a=2,
当a=-1时,l1:-x+2y+6=0,l2:x+2y=0,显然l1∥l2.
当a=2时,l1:x+y+3=0,l2:x+y+3=0,显然l1与l2重合,
∴当a≠-1且a≠2时,l1与l2相交,
由a×1+2(a-1)=0可解得a=
,此时l1⊥l2;
故答案为:a≠-1且a≠2;=
;a=2;a=-1
当a=-1时,l1:-x+2y+6=0,l2:x+2y=0,显然l1∥l2.
当a=2时,l1:x+y+3=0,l2:x+y+3=0,显然l1与l2重合,
∴当a≠-1且a≠2时,l1与l2相交,
由a×1+2(a-1)=0可解得a=
| 2 |
| 3 |
故答案为:a≠-1且a≠2;=
| 2 |
| 3 |
点评:本题考查两直线的位置关系,判平行与垂直是关键,属基础题.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
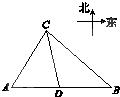 如图,港口A北偏东30°方向的C处有一检查站,港口正东方向的B处有一轮船,距离检查站7海里,该轮船从B处沿正西方向航行3海里后到达D处观测站,已知观测站与检查站距离5海里,则此时轮船离港口A有
如图,港口A北偏东30°方向的C处有一检查站,港口正东方向的B处有一轮船,距离检查站7海里,该轮船从B处沿正西方向航行3海里后到达D处观测站,已知观测站与检查站距离5海里,则此时轮船离港口A有