题目内容
5.已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的左、右焦点分别为F1,F2,过F1且与x轴垂直的直线交椭圆于A、B两点,直线AF2与椭圆的另一个交点为C,若$\overrightarrow{A{F_2}}+2\overrightarrow{C{F_2}}$=0,则椭圆的离心率为$\frac{\sqrt{5}}{5}$.分析 由题意画出图形,求出A的坐标,结合向量加法的坐标运算,求得C的坐标,代入椭圆方程可解e的值.
解答 解:如图,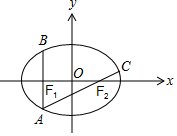
由题意,A(-c,-$\frac{{b}^{2}}{a}$),F2(c,0),C(x,y),
∵$\overrightarrow{A{F}_{2}}$+2$\overrightarrow{C{F}_{2}}$=0,(2c,$\frac{{b}^{2}}{a}$)+2(-x+c,-y)=0,
∴y=$\frac{{b}^{2}}{2a}$,x=2c.
∴C(2c,$\frac{{b}^{2}}{2a}$),代入椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$,$\frac{4{c}^{2}}{{a}^{2}}$+$\frac{{b}^{2}}{4{a}^{2}}$=1,由b2=a2-c2,
整理得:5c2=a2,解得e=$\sqrt{\frac{{c}^{2}}{{a}^{2}}}$=$\frac{\sqrt{5}}{5}$.
椭圆的离心率$\frac{\sqrt{5}}{5}$.
故答案为:$\frac{\sqrt{5}}{5}$.
点评 本题考查椭圆的简单性质,考查了平面向量的坐标运算在求解圆锥曲线问题中的应用,是中档题.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
15.某班级为了进行户外拓展游戏,组成红、蓝、黄3个小队.甲、乙两位同学各自等可能地选择其中一个小队,则他们选到同一小队的概率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
15.已知点A是直角三角形ABC的直角顶点,且A(2a,2),B(-4,a),C(2a+2,2),则△ABC的外接圆的方程是( )
| A. | x2+(y-3)2=5 | B. | x2+(y+3)2=5 | C. | (x-3)2+y2=5 | D. | (x+3)2+y2=5 |

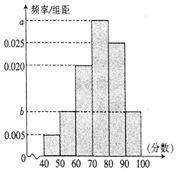 某校从高一年级学生中随机抽取40名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100]后得到如图所示的频率分布直方图,其中前三段的频率成等比数列.
某校从高一年级学生中随机抽取40名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100]后得到如图所示的频率分布直方图,其中前三段的频率成等比数列.