题目内容

15．已知点A是直角三角形ABC的直角顶点，且A（2a，2），B（-4，a），C（2a+2，2），则△ABC的外接圆的方程是（　　）
A．x2+（y-3）2=5B．x2+（y+3）2=5C．（x-3）2+y2=5D．（x+3）2+y2=5

分析 根据点A是直角三角形ABC的直角顶点，求出a，B，C的坐标求得圆心的坐标和圆的半径，则圆的方程可得．

解答 解：由题意，2a=-4，∴a=-2
∴圆的半径为$\frac{BC}{2}$=$\frac{\sqrt{（-4+2）^{2}+（-2-2）^{2}}}{2}$=$\sqrt{5}$，圆心为（-3，0）
∴圆的方程为（x+3）2+y2=5
故选D．

点评 本题主要考查了圆的标准方程，直线斜率的运用．解题的关键求得圆的圆心和半径．

练习册系列答案
相关题目
5．已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（{a＞b＞0}）$的左、右焦点分别为F1，F2，过F1且与x轴垂直的直线交椭圆于A、B两点，直线AF2与椭圆的另一个交点为C，若$\overrightarrow{A{F_2}}+2\overrightarrow{C{F_2}}$=0，则椭圆的离心率为$\frac{\sqrt{5}}{5}$．
6．已知函数f（x）=xex-m有2个零点都大于-2，则实数m的取值范围是（-$\frac{1}{e}$，-$\frac{2}{{e}^{2}}$）．
3．已知全集U={1，2，3，4}，集合A={1，4}，B={3，4}，则∁U（A∪B）={2}．
10．如图所示，向量$\overrightarrow{O{Z_1}}，\overrightarrow{O{Z_2}}$所对应的复数分别为Z1，Z2，则Z1•Z2=（　　）
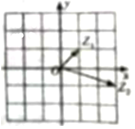
A．4+2iB．2+iC．2+2iD．3+i
20．已知F1、F2分别是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$的左、右焦点，P为双曲线右支上的任意一点且$\frac{|P{F}_{1}{|}^{2}}{|P{F}_{2}|}$=8a，则双曲线离心率的取值范围是（　　）
A．（1，3]B．[3，+∞）C．（1，2]D．[2，+∞）
6．设a＞0，b＞0，若$\sqrt{2}$是2a与2b的等比中项，求a2+2b2的取值范围．
3．已知双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0），直线l：y=2x-2，若直线l平行于双曲线C的一条渐近线且经过C的一个顶点，则双曲线C的焦点到渐近线的距离为（　　）
A．1B．2C．$\sqrt{5}$D．4
4．设Sn，Tn分别是数列{an}和{bn}的前n项和，已知对于任意n∈N*，都有3an=2Sn+3，数列{bn}是等差数列，且T5=25，b10=19．
（Ⅰ）求数列{an}和{bn}的通项公式；
（Ⅱ）设cn=$\frac{{{a}_{n}b}_{n}}{n（n+1）}$，求数列{cn}的前n项和Rn．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网