题目内容
20.函数f(x)=ln(x+1)+$\frac{1}{{\sqrt{2-{x^2}}}}$的定义域是(-1,$\sqrt{2}$).分析 根据对数的真数大于0,二次根式被开方数大于或等于0,分母不为0,列出不等式组求解集即可.
解答 解:函数f(x)=ln(x+1)+$\frac{1}{{\sqrt{2-{x^2}}}}$,
∴$\left\{\begin{array}{l}{x+1>0}\\{2{-x}^{2}>0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x>-1}\\{-\sqrt{2}<x<\sqrt{2}}\end{array}\right.$,
即-1<x<$\sqrt{2}$;
∴f(x)的定义域为(-1,$\sqrt{2}$).
故答案为:(-1,$\sqrt{2}$).
点评 本题考查了求函数的定义域应用问题,是基础题.

练习册系列答案
相关题目
8.已知等比数列{an},且a6+a8=4,则a8(a4+2a6+a8)的值为( )
| A. | 2 | B. | 4 | C. | 8 | D. | 16 |
9.将一条均匀木棍随机折成两段,则其中一段大于另一段三倍的概率为( )
| A. | $\frac{3}{4}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |
10.如图所示,向量$\overrightarrow{O{Z_1}},\overrightarrow{O{Z_2}}$所对应的复数分别为Z1,Z2,则Z1•Z2=( )
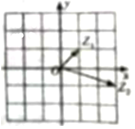

| A. | 4+2i | B. | 2+i | C. | 2+2i | D. | 3+i |
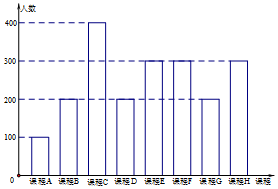 为了响应教育部颁布的《关于推进中小学生研学旅行的意见》,某校计划开设八门研学旅行课程,并对全校学生的选课意向进行调查(调查要求全员参与,每个学生必须从八门课程中选出唯一一门课程).本次调查结果如下.图中,课程A,B,C,D,E为人文类课程,课程F,G,H为自然科学类课程.为进一步研究学生选课意向,结合上面图表,采取分层抽样方法从全校抽取1%的学生作为研究样本组(以下简称“组M”).
为了响应教育部颁布的《关于推进中小学生研学旅行的意见》,某校计划开设八门研学旅行课程,并对全校学生的选课意向进行调查(调查要求全员参与,每个学生必须从八门课程中选出唯一一门课程).本次调查结果如下.图中,课程A,B,C,D,E为人文类课程,课程F,G,H为自然科学类课程.为进一步研究学生选课意向,结合上面图表,采取分层抽样方法从全校抽取1%的学生作为研究样本组(以下简称“组M”).