题目内容
设函数f(x)=
-aln(1+x),g(x)=ln(1+x)-bx.
(1)若函数f(x)在x=0处有极值,求函数f(x)的最大值;
(2)是否存在实数b,使得关于x的不等式g(x)<0在(0,+∞)上恒成立?若存在,求出b的取值范围;若不存在,说明理由;
(3)证明:不等式-1<
-lnn≤
(n=1,2.…).
| x |
| 1+x |
(1)若函数f(x)在x=0处有极值,求函数f(x)的最大值;
(2)是否存在实数b,使得关于x的不等式g(x)<0在(0,+∞)上恒成立?若存在,求出b的取值范围;若不存在,说明理由;
(3)证明:不等式-1<
| n |
 |
| k=1 |
| k |
| k2+1 |
| 1 |
| 2 |
考点:利用导数研究函数的单调性,利用导数求闭区间上函数的最值
专题:导数的综合应用
分析:(1)由已知得:f′(x)=
-
,且函数f(x)在x=0处有极值,得a=1,从而求出函数的表达式,找出单调区间求出最值;
(2)由已知得:g′(x)=
-b再对b分情况讨论:①若b≥1,②若b≤0,③若0<b<1综合得出b的取值范围是x∈[1,+∞);
(3)由前两问综合得出.
| 1 |
| (1+x)2 |
| a |
| 1+x |
(2)由已知得:g′(x)=
| 1 |
| 1+x |
(3)由前两问综合得出.
解答:
解析:(1)由已知得:f′(x)=
-
,且函数f(x)在x=0处有极值
∴f′(0)=
-
=0,
∴a=1
∴f(x)=
-ln(1+x),
∴f′(x)=
-
=
当x∈(-1,0)时,f'(x)>0,f(x)单调递增;
当x∈(0,+∞)时,f'(x)<0,f(x)单调递减;
∴函数f(x)的最大值为f(0)=0.
(2)由已知得:g′(x)=
-b
①若b≥1,则x∈[0,+∞)时,
g′(x)=
-b≤0
∴g(x)=ln(1+x)-bx在[0,+∞)上为减函数,
∴g(x)=ln(1+x)-bx<g(0)=0在(0,+∞)上恒成立;
②若b≤0,则x∈[0,+∞)时,
g′(x)=
-b>0
∴g(x)=ln(1+x)-bx在[0,+∞)上为增函数,
∴g(x)=ln(1+x)-bx>g(0)=0,
不能使g(x)<0在(0,+∞)上恒成立;
③若0<b<1,则g′(x)=
-b=0时,
x=
-1,
当x∈[0,
-1)时,g'(x)≥0,
∴g(x)=ln(1+x)-bx在[0,
-1)上为增函数,
此时g(x)=ln(1+x)-bx>g(0)=0,
∴不能使g(x)<0在(0,+∞)上恒成立;
综上所述,b的取值范围是x∈[1,+∞).
(3)由(1)、(2)得:
<ln(1+x)<x(x>0)
取x=
得:
<ln(1+
)<
.
令xn=
-lnn,
则x1=
,xn-xn-1=
-ln(1+
)<
-
=-
<0.
因此xn<xn-1<…<x1=
.
又lnn=
[lnk-ln(k-1)]+ln1=
ln(1+
),
故xn=
-
ln(1+
)=
[
-ln(1+
)]+
>
(
-
)=-
≥
=-1+
>-1.
| 1 |
| (1+x)2 |
| a |
| 1+x |
∴f′(0)=
| 1 |
| (1+0)2 |
| a |
| 1+0 |
∴a=1
∴f(x)=
| x |
| 1+x |
∴f′(x)=
| 1 |
| (1+x)2 |
| 1 |
| 1+x |
| -x |
| (1+x)2 |
当x∈(-1,0)时,f'(x)>0,f(x)单调递增;
当x∈(0,+∞)时,f'(x)<0,f(x)单调递减;
∴函数f(x)的最大值为f(0)=0.
(2)由已知得:g′(x)=
| 1 |
| 1+x |
①若b≥1,则x∈[0,+∞)时,
g′(x)=
| 1 |
| 1+x |
∴g(x)=ln(1+x)-bx在[0,+∞)上为减函数,
∴g(x)=ln(1+x)-bx<g(0)=0在(0,+∞)上恒成立;
②若b≤0,则x∈[0,+∞)时,
g′(x)=
| 1 |
| 1+x |
∴g(x)=ln(1+x)-bx在[0,+∞)上为增函数,
∴g(x)=ln(1+x)-bx>g(0)=0,
不能使g(x)<0在(0,+∞)上恒成立;
③若0<b<1,则g′(x)=
| 1 |
| 1+x |
x=
| 1 |
| b |
当x∈[0,
| 1 |
| b |
∴g(x)=ln(1+x)-bx在[0,
| 1 |
| b |
此时g(x)=ln(1+x)-bx>g(0)=0,
∴不能使g(x)<0在(0,+∞)上恒成立;
综上所述,b的取值范围是x∈[1,+∞).
(3)由(1)、(2)得:
| x |
| 1+x |
取x=
| 1 |
| n |
| 1 |
| 1+n |
| 1 |
| n |
| 1 |
| n |
令xn=
| n |
 |
| k=1 |
| k |
| k2+1 |
则x1=
| 1 |
| 2 |
| n |
| n2+1 |
| 1 |
| n-1 |
| n |
| n2+1 |
| 1 |
| n |
| 1 |
| (n2+1)n |
因此xn<xn-1<…<x1=
| 1 |
| 2 |
又lnn=
| n |
 |
| k=2 |
| n-1 |
 |
| k=1 |
| 1 |
| k |
故xn=
| n |
 |
| k=1 |
| k |
| k2+1 |
| n-1 |
 |
| k=1 |
| 1 |
| k |
| n-1 |
 |
| k=1 |
| k |
| k2+1 |
| 1 |
| k |
| n |
| n2+1 |
>
| n-1 |
 |
| k=1 |
| k |
| k2+1 |
| 1 |
| k |
| n-1 |
 |
| k=1 |
| 1 |
| (k2+1)k |
| n-1 |
 |
| k=1 |
| 1 |
| (k+1)k |
| 1 |
| n |
点评:本题考察了函数的最值问题,函数的单调性,导数的应用,不等式的证明,渗透了分类讨论思想,是一道综合题.

练习册系列答案
相关题目
已知
、
为非零不共线向量,向量8
-k
与-k
+
共线,则k=( )
| a |
| b |
| a |
| b |
| a |
| b |
A、2
| ||
B、-2
| ||
C、±2
| ||
| D、8 |
 如图,在四棱锥P-ABCD中,底面ABCD是菱形,PA=PB,且侧面PAB⊥平面ABCD,点E是棱AB的中点.
如图,在四棱锥P-ABCD中,底面ABCD是菱形,PA=PB,且侧面PAB⊥平面ABCD,点E是棱AB的中点.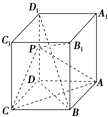 如图,长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,点P为DD1的中点.求证:
如图,长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,点P为DD1的中点.求证: