题目内容
已知箱中装有4个白球和5个黑球,且规定:取出一个白球得2分,取出一个黑球得1分.现从该箱中任取(无放回,且每球取到的机会均等)3个球,记随机变量X为取出此3球所得分数之和.
(1)求X的分布列;
(2)求得分大于4的概率.
(1)求X的分布列;
(2)求得分大于4的概率.
考点:相互独立事件的概率乘法公式,互斥事件的概率加法公式
专题:概率与统计
分析:(1)X的可能取值有:3,4,5,6,求出相应的概率可得所求X的分布列;
(2)由(1)以及P(X>4)=P(X=5)+P(X=6),即可得到结论.
(2)由(1)以及P(X>4)=P(X=5)+P(X=6),即可得到结论.
解答:
解 (1)由题意得X取3,4,5,6,且
P(X=3)=
=
,P(X=4)=
=
,
P(X=5)=
=
,P(X=6)=
=
.
所以X的分布列为
(2)P(X>4)=P(X=5)+P(X=6)=
+
=
.
P(X=3)=
| ||
|
| 5 |
| 42 |
| ||||
|
| 10 |
| 21 |
P(X=5)=
| ||||
|
| 5 |
| 14 |
| ||
|
| 1 |
| 21 |
所以X的分布列为
| X | 3 | 4 | 5 | 6 | ||||||||
| P |
|
|
|
|
| 5 |
| 14 |
| 1 |
| 21 |
| 5 |
| 42 |
点评:本题主要考查随机事件的概率和随机变量的分布列,同时考查抽象概括、运算能力,属于中档题.

练习册系列答案
相关题目
在四边形ABCD中,
=(2,4),
=(-6,3),则该四边形的面积为( )
| AC |
| BD |
A、3
| ||
B、2
| ||
| C、5 | ||
| D、15 |
函数y=x2在区间[1,2]上的平均变化率为( )
| A、4 | B、5 | C、2 | D、3 |
 如图,在四棱柱ABCD-A1B1C1D1中,底面ABCD和侧面BCC1B1都是矩形,E是CD的中点,D1E⊥CD,AB=2BC=2.
如图,在四棱柱ABCD-A1B1C1D1中,底面ABCD和侧面BCC1B1都是矩形,E是CD的中点,D1E⊥CD,AB=2BC=2.
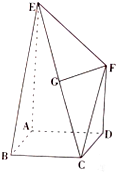 如图,四边形ABCD是边长为2的正方形,AE⊥面ABCD,DF∥AE,AE=4,G为EC的中点,且GF∥面ABCD.
如图,四边形ABCD是边长为2的正方形,AE⊥面ABCD,DF∥AE,AE=4,G为EC的中点,且GF∥面ABCD.