题目内容
设{an}是首项为1,公差为d的等差数列,bn=anqn,其中q∈R,且q≠0.
(1)试研究:{bn}(n∈N*)是否为等比数列?请说明理由;
(2)请类比等比数列前n项和公式的推导过程,求数列{bn}的前n项和Sn.
(1)试研究:{bn}(n∈N*)是否为等比数列?请说明理由;
(2)请类比等比数列前n项和公式的推导过程,求数列{bn}的前n项和Sn.
考点:数列的求和,等比数列的性质
专题:等差数列与等比数列
分析:(1)由等差数列的通项公式得an=1+(n-1)d,从而得到
=
=
q,由此求出d=0时,{bn}(n∈N*)是等比数列;d≠0时,{bn}(n∈N*)不是等比数列.
(2)由bn=anqn=[1+(n-1)d]qn,利用错位相减法能求出数列{bn}的前n项和Sn.
| bn+1 |
| bn |
| (1+nd)qn+1 |
| [1+(n-1)d]qn |
| 1+nd |
| 1+(n-1)d |
(2)由bn=anqn=[1+(n-1)d]qn,利用错位相减法能求出数列{bn}的前n项和Sn.
解答:
解:(1)∵{an}是首项为1,公差为d的等差数列,
∴an=1+(n-1)d,
∴bn=anqn=[1+(n-1)d]qn,
∴
=
=
q,
∴d=0时,{bn}(n∈N*)是等比数列;
d≠0时,{bn}(n∈N*)不是等比数列.
(2)∵bn=anqn=[1+(n-1)d]qn,
∴Sn=q+(1+d)q2+(1+2d)q3+…+[1+(n-1)d]qn,①
∴qSn=q2+(1+d)q3+(1+2d)q4+…+[1+(n-1)d]qn+1 ,②
①-②,得:(1-q)Sn=q+dq2+dq3+dq4+…+dqn-[1+(n-1)d]qn+1
=q+d×
-[1+(n-1)d]qn+1 ,
∴Sn =+
d-
.
∴an=1+(n-1)d,
∴bn=anqn=[1+(n-1)d]qn,
∴
| bn+1 |
| bn |
| (1+nd)qn+1 |
| [1+(n-1)d]qn |
| 1+nd |
| 1+(n-1)d |
∴d=0时,{bn}(n∈N*)是等比数列;
d≠0时,{bn}(n∈N*)不是等比数列.
(2)∵bn=anqn=[1+(n-1)d]qn,
∴Sn=q+(1+d)q2+(1+2d)q3+…+[1+(n-1)d]qn,①
∴qSn=q2+(1+d)q3+(1+2d)q4+…+[1+(n-1)d]qn+1 ,②
①-②,得:(1-q)Sn=q+dq2+dq3+dq4+…+dqn-[1+(n-1)d]qn+1
=q+d×
| q2(1-qn-1) |
| 1-q |
∴Sn =+
| q2(1-qn-1) |
| (1-q)2 |
| [1+(n-1)d]qn+1 |
| 1-q |
点评:本题考查等比数列的判断,考查数列的前n项和的求法,解题时要认真审题,注意错位相减求和法的合理运用.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
复数(3m-2)+(m-1)i是虚数,则实数m应满足的条件是( )
| A、m≠1 | ||
B、m≠
| ||
| C、m=1 | ||
D、m=
|

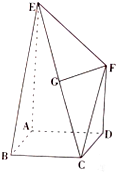 如图,四边形ABCD是边长为2的正方形,AE⊥面ABCD,DF∥AE,AE=4,G为EC的中点,且GF∥面ABCD.
如图,四边形ABCD是边长为2的正方形,AE⊥面ABCD,DF∥AE,AE=4,G为EC的中点,且GF∥面ABCD.