题目内容
4.已知点P(0,-2),椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\;(a>b>0)$的离心率为$\frac{{\sqrt{2}}}{2}$,F是椭圆E的右焦点,直线PF的斜率为2,O为坐标原点.(1)求椭圆E的方程;
(2)直线l被圆O:x2+y2=3截得的弦长为3,且与椭圆E交于A、B两点,求△AOB面积的最大值.
分析 (1)椭圆离心率及直线的斜率公式求得a和b的值,即可求得椭圆的方程;
(2)分类,当直线的斜率不存在,求得丨AB丨,根据三角形的面积公式,求得△AOB面积,当直线的斜率存在时,由点到直线的距离公式求得${m^2}=\frac{3}{4}({k^2}+1)$,将直线方程代入椭圆方程,由韦达定理,弦长公式及基本不等式的性质,即可求得△AOB面积的最大值.
解答 解:(1)设F(c,0),由已知得,直线PF的斜率k=$\frac{2}{c}=2$,得c=1,又$\frac{c}{a}=\frac{{\sqrt{2}}}{2}$,
则$a=\sqrt{2}$,b=1,
故椭圆E的方程为$\frac{x^2}{2}+{y^2}=1$…(3分)
(2)记点O到直线l的距离为d,则$d=\sqrt{{r^2}-{{(\frac{3}{2})}^2}}=\frac{{\sqrt{3}}}{2}$,
①当直线l与y轴平行时,直线l的方程为$x=±\frac{{\sqrt{3}}}{2}$,易求$|AB|=\frac{{\sqrt{10}}}{2}$,
∴${S_{△AOB}}=\frac{1}{2}|AB|d=\frac{{\sqrt{30}}}{8}$,…(4分)
②当直线l与y轴不平行时,设直线l的方程为y=kx+m,A(x1,y1),B(x2,y2),
由已知得$d=\frac{|m|}{{\sqrt{{k^2}+1}}}=\frac{{\sqrt{3}}}{2}$,∴${m^2}=\frac{3}{4}({k^2}+1)$,.…(5分)
由$\left\{\begin{array}{l}y=kx+m\\ \frac{x^2}{2}+{y^2}=1\end{array}\right.$得(2k2+1)x2+4kmx+2(m2-1)=0,又△=10k2+2>0,
∴${x_1}+{x_2}=-\frac{4km}{{2{k^2}+1}}$,${x_1}{x_2}=\frac{{2({m^2}-1)}}{{2{k^2}+1}}$,…(6分)
∴$|AB|=\sqrt{1+{k^2}}|{x_1}-{x_2}|=\frac{{\sqrt{2(1+{k^2})(5{k^2}+1)}}}{{2{k^2}+1}}$,…(7分)
${S_{△AOB}}=\frac{1}{2}|AB|d=\frac{{\sqrt{3}}}{4}|AB|=\frac{{\sqrt{3}}}{4}×\frac{{\sqrt{2(1+{k^2})(5{k^2}+1)}}}{{2{k^2}+1}}=\frac{{\sqrt{2}}}{4}×\frac{{\sqrt{3(1+{k^2})(5{k^2}+1)}}}{{2{k^2}+1}}$,
$≤\frac{{\sqrt{2}}}{4}×\frac{{\frac{1}{2}(3+3{k^2}+5{k^2}+1)}}{{2{k^2}+1}}=\frac{{\sqrt{2}}}{2}$,当且仅当k=±1时取等号,…(9分)
综上当k=±1时,△AOB面积的最大值为$\frac{{\sqrt{2}}}{2}$…(10分)
点评 本题考查椭圆的标准方程及简单性质,考查直线与椭圆的位置关系,韦达定理,弦长公式及基本不等式的应用,考查计算能力,属于中档题.

 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案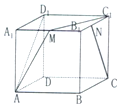 在棱长为1的正方体ABCD-A1B1C1D1中,M和N分别为A1B1和B1C1的中点,那么直线AM与CN所成角的余弦值是( )
在棱长为1的正方体ABCD-A1B1C1D1中,M和N分别为A1B1和B1C1的中点,那么直线AM与CN所成角的余弦值是( )| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $\frac{{\sqrt{10}}}{10}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
| A. | $x=-\frac{1}{2}$ | B. | $y=-\frac{1}{2}$ | C. | $x=\frac{1}{2}$ | D. | $y=\frac{1}{2}$ |
| A. | a=$\sqrt{3}$ | B. | a=-$\sqrt{3}$ | C. | a=-1 | D. | a=1 |
| A. | {x|x≥-1} | B. | {x|x>-1} | C. | {x|x≥0} | D. | {x|x>0} |
| A. | (-∞,-$\frac{3}{4}$)∪(-$\frac{1}{4}$,+∞) | B. | (-∞,-$\frac{3}{4}$) | C. | (-$\frac{1}{4}$,+∞) | D. | (-$\frac{3}{4}$,-$\frac{1}{4}$) |
 如图,四棱锥P-ABCD中,底面ABCD是矩形,面PAD⊥底面ABCD,且△PAD是边长为2的等边三角形,PC=$\sqrt{13}$,M在PC上,且PA∥面MBD.
如图,四棱锥P-ABCD中,底面ABCD是矩形,面PAD⊥底面ABCD,且△PAD是边长为2的等边三角形,PC=$\sqrt{13}$,M在PC上,且PA∥面MBD.