题目内容
1．已知集合A={-2，-1，0，1，2}，∁RB={x|（x-1）（x+2）≥0}，则A∩B=（ ）| A． | {-1，0，1} | B． | {-1，0} | C． | {-2，-1，0} | D． | {-2，1，2} |
分析 根据补集与交集的定义，即可求出运算结果．
解答 解：集合A={-2，-1，0，1，2}，
∁RB={x|（x-1）（x+2）≥0}，
∴B={x|（x-1）（x+2）＜0}={x|-2＜x＜1}．
∴A∩B={-1，0}．
故选：B．
点评 本题考查了解不等式与集合的运算问题，是基础题．
练习册系列答案
相关题目
11．函数$f（x）=3sin（2x+\frac{π}{2}）$是（ ）
| A． | 周期为$\frac{π}{2}$的奇函数 | B． | 周期为$\frac{π}{2}$的偶函数 | ||
| C． | 周期为π的奇函数 | D． | 周期为π的偶函数 |
12．已知抛物线y2=2px（p＞0）过点A（2，2），则它的准线方程是（ ）
| A． | $x=-\frac{1}{2}$ | B． | $y=-\frac{1}{2}$ | C． | $x=\frac{1}{2}$ | D． | $y=\frac{1}{2}$ |
9．复数z=（a+i）（-3+ai）（a∈R），若z＜0，则a的值是（ ）
| A． | a=$\sqrt{3}$ | B． | a=-$\sqrt{3}$ | C． | a=-1 | D． | a=1 |
如图，四棱锥P-ABCD中，底面ABCD是矩形，面PAD⊥底面ABCD，且△PAD是边长为2的等边三角形，PC=$\sqrt{13}$，M在PC上，且PA∥面MBD．
6．
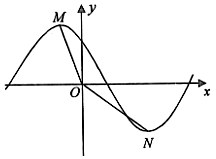将函数y=$\sqrt{3}$sin（$\frac{π}{4}$x）的图象向左平移3个单位，得函数y=$\sqrt{3}$sin（$\frac{π}{4}$x+φ）（|φ|＜π）的图象（如图），点M，N分别是函数f（x）图象上y轴两侧相邻的最高点和最低点，设∠MON=θ，则tan（φ-θ）的值为（ ）
将函数y=$\sqrt{3}$sin（$\frac{π}{4}$x）的图象向左平移3个单位，得函数y=$\sqrt{3}$sin（$\frac{π}{4}$x+φ）（|φ|＜π）的图象（如图），点M，N分别是函数f（x）图象上y轴两侧相邻的最高点和最低点，设∠MON=θ，则tan（φ-θ）的值为（ ）| A． | 1-$\sqrt{3}$ | B． | 2-$\sqrt{3}$ | C． | 1+$\sqrt{3}$ | D． | -2+$\sqrt{3}$ |
13．已知集合A={x|x（x+1）≤0}，集合B={x|x＞0}，则A∪B=（ ）
| A． | {x|x≥-1} | B． | {x|x＞-1} | C． | {x|x≥0} | D． | {x|x＞0} |
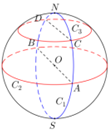如图，N、S是球O直径的两个端点，圆C1是经过N和S点的大圆，圆C2和圆C3分别是所在平面与NS垂直的大圆和小圆，圆C1和C2交于点A、B，圆C1和C3交于点C、D，设a、b、c分别表示圆C1上劣弧CND的弧长、圆C2上半圆弧AB的弧长、圆C3上半圆弧CD的弧长，则a、b、c的大小关系为（ ）