题目内容
6.设f(x)是定义在R上的奇函数,当x>0时,f(x)=2x-3,则不等式f(x)<-5的解为(-∞,-3).分析 根据函数奇偶性的性质求出当x<0的解析式,讨论x>0,x<0,x=0,解不等式即可.
解答 解:若x<0,则-x>0,
∵当x>0时,f(x)=2x-3,
∴当-x>0时,f(-x)=2-x-3,
∵f(x)是定义在R上的奇函数,
∴f(-x)=2-x-3=-f(x),
则f(x)=-2-x+3,x<0,
当x>0时,不等式f(x)<-5等价为2x-3<-5即2x<-2,无解,不成立;
当x<0时,不等式f(x)<-5等价为-2-x+3<-5即2-x>8,
得-x>3,即x<-3;
当x=0时,f(0)=0,不等式f(x)<-5不成立,
综上,不等式的解为x<-3.
故不等式的解集为(-∞,-3).
故答案为(-∞,-3).
点评 本题主要考查不等式的解集的求解,根据函数奇偶性的性质求出函数的解析式是解决本题的关键.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
17.一个棱长为$6\sqrt{2}$的正四面体纸盒内放一个正方体,若正方体可以在纸盒内任意转动,则正方体棱长的最大值为( )
| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | 3 |
14.已知f(x)是定义在R上的偶函数,且在区间(-∞,0)上单调递减,若实数a满足f(3|2a+1|)>f(-$\sqrt{3}$),则a的取值范围是( )
| A. | (-∞,-$\frac{3}{4}$)∪(-$\frac{1}{4}$,+∞) | B. | (-∞,-$\frac{3}{4}$) | C. | (-$\frac{1}{4}$,+∞) | D. | (-$\frac{3}{4}$,-$\frac{1}{4}$) |
11.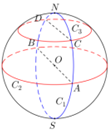 如图,N、S是球O直径的两个端点,圆C1是经过N和S点的大圆,圆C2和圆C3分别是所在平面与NS垂直的大圆和小圆,圆C1和C2交于点A、B,圆C1和C3交于点C、D,设a、b、c分别表示圆C1上劣弧CND的弧长、圆C2上半圆弧AB的弧长、圆C3上半圆弧CD的弧长,则a、b、c的大小关系为( )
如图,N、S是球O直径的两个端点,圆C1是经过N和S点的大圆,圆C2和圆C3分别是所在平面与NS垂直的大圆和小圆,圆C1和C2交于点A、B,圆C1和C3交于点C、D,设a、b、c分别表示圆C1上劣弧CND的弧长、圆C2上半圆弧AB的弧长、圆C3上半圆弧CD的弧长,则a、b、c的大小关系为( )
 如图,N、S是球O直径的两个端点,圆C1是经过N和S点的大圆,圆C2和圆C3分别是所在平面与NS垂直的大圆和小圆,圆C1和C2交于点A、B,圆C1和C3交于点C、D,设a、b、c分别表示圆C1上劣弧CND的弧长、圆C2上半圆弧AB的弧长、圆C3上半圆弧CD的弧长,则a、b、c的大小关系为( )
如图,N、S是球O直径的两个端点,圆C1是经过N和S点的大圆,圆C2和圆C3分别是所在平面与NS垂直的大圆和小圆,圆C1和C2交于点A、B,圆C1和C3交于点C、D,设a、b、c分别表示圆C1上劣弧CND的弧长、圆C2上半圆弧AB的弧长、圆C3上半圆弧CD的弧长,则a、b、c的大小关系为( )| A. | b>a=c | B. | b=c>a | C. | b>a>c | D. | b>c>a |
18.10、(文)若关于x的不等式x3-3x+3+a≤0恒成立,其中-2≤x≤3,则实数a的最大值为( )
| A. | 1 | B. | -1 | C. | -5 | D. | -21 |
15.已知全集U={1,2,3,4},若A={1,3},则∁UA=( )
| A. | {1,2} | B. | {1,4} | C. | {2,3} | D. | {2,4} |
 如图,四棱锥P-ABCD中,底面ABCD是矩形,面PAD⊥底面ABCD,且△PAD是边长为2的等边三角形,PC=$\sqrt{13}$,M在PC上,且PA∥面MBD.
如图,四棱锥P-ABCD中,底面ABCD是矩形,面PAD⊥底面ABCD,且△PAD是边长为2的等边三角形,PC=$\sqrt{13}$,M在PC上,且PA∥面MBD.
 的奇偶性;
的奇偶性; ,函数
,函数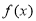 在区间
在区间 上为减函数,求实数a的取值范围.
上为减函数,求实数a的取值范围.