题目内容
5.已知正项数列{an}满足a1=1,(n+2)an+12-(n+1)an2+anan+1=0,则an=$\frac{2}{n+1}$.分析 把数列递推式变形,可得(n+2)•$(\frac{{a}_{n+1}}{{a}_{n}})^{2}+\frac{{a}_{n+1}}{{a}_{n}}=n+1$,即$\frac{{a}_{n+1}}{{a}_{n}}=\frac{n+1}{n+2}$.然后利用累积法得答案.
解答 解:由(n+2)an+12-(n+1)an2+anan+1=0,得
(n+2)•$(\frac{{a}_{n+1}}{{a}_{n}})^{2}+\frac{{a}_{n+1}}{{a}_{n}}=n+1$,即
$\frac{{a}_{n+1}}{{a}_{n}}=\frac{n+1}{n+2}$.
∴${a}_{n}=\frac{{a}_{n}}{{a}_{n-1}}•\frac{{a}_{n-1}}{{a}_{n-2}}•…•\frac{{a}_{2}}{{a}_{1}}•{a}_{1}$
=$\frac{n}{n+1}•\frac{n-1}{n}•…•\frac{2}{3}•1=\frac{2}{n+1}$.
故答案为:$\frac{2}{n+1}$.
点评 本题考查数列递推式,考查了累积法求数列的通项公式,是中档题.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
16.三棱锥P-ABC三条侧棱两两垂直,三条侧棱长分别为1,$\sqrt{5}$,$\sqrt{10}$,则该三棱锥的外接球体积为( )
| A. | $\frac{32}{3}$π | B. | $\frac{16}{3}$π | C. | 32π | D. | 16π |
13.若函数f(x)同时满足以下三个性质:①f(x)的最小正周期为π;②对任意的x∈R,都有f(x-$\frac{π}{4}$)+f(-x)=0;③f(x)在($\frac{π}{4}$,$\frac{π}{2}$)上是减函数,则f(x)的解析式可能是( )
| A. | f(x)=sin2x+cos2x | B. | f(x)=sin2x | C. | f(x)=tan(x+$\frac{π}{8}$) | D. | f(x)=cos2x |
15.已知O是平面内任意一点,α是任意角,下列等式一定可以判定A,B,C三点共线的是( )
| A. | $\overrightarrow{OC}$=sinα$\overrightarrow{OA}$+cosα$\overrightarrow{OB}$ | B. | $\overrightarrow{OC}$=sin2α$\overrightarrow{OA}$+cos2α$\overrightarrow{OB}$ | ||
| C. | $\overrightarrow{OC}$=sinα$\overrightarrow{OA}$-cosα$\overrightarrow{OB}$ | D. | $\overline{OC}$=sin2α$\overrightarrow{OA}$-cos2α$\overrightarrow{OB}$ |
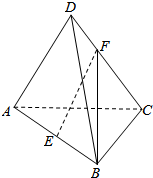 如图,在空间四边形ABCD中,E是线段AB的中点.
如图,在空间四边形ABCD中,E是线段AB的中点.