题目内容
已知函数f（x）=x2-2a2lnx（a＞0）．
（Ⅰ）求函数f（x）的单调区间；
（Ⅱ）记函数f（x）的最小值为M，求证：M≤1．
（Ⅰ）求函数f（x）的单调区间；
（Ⅱ）记函数f（x）的最小值为M，求证：M≤1．
考点：导数在最大值、最小值问题中的应用,利用导数研究函数的单调性
专题：综合题,导数的综合应用
分析：（Ⅰ）确定函数的定义域，求导函数，利用导数的正负，可得函数f（x）的单调区间；
（Ⅱ）由（Ⅰ）知，f（x）的最小值M=a2-2a2lna，令g（x）=x2-2x2lnx（x＞0）求出函数的最大值，即可得出结论．
（Ⅱ）由（Ⅰ）知，f（x）的最小值M=a2-2a2lna，令g（x）=x2-2x2lnx（x＞0）求出函数的最大值，即可得出结论．
解答：
（Ⅰ）解：f（x）=x2-2a2lnx（a＞0）的定义域为（0，+∞）．
f′(x)=2x-
=
=
．…（2分）
令f'（x）=0，解得x=a或x=-a（舍）．
当x在（0，+∞）内变化时，f'（x），f（x）的变化情况如下：
由上表知，f（x）的单调递增区间为（a，+∞）；f（x）的单调递减区间为（0，a）．…（5分）
（Ⅱ）证明：由（Ⅰ）知，f（x）的最小值M=a2-2a2lna．…（6分）
令g（x）=x2-2x2lnx（x＞0），则g'（x）=2x-4xlnx-2x=-4xlnx．
令g'（x）=0，解得x=1．…（8分）
当x在（0，+∞）内变化时，g'（x），g（x）的变化情况如下：
所以函数g（x）的最大值为1，即g（x）≤1．
因为a＞0，所以 M=a2-2a2lna≤1．…（11分）
f′(x)=2x-
| 2a2 |
| x |
| 2x2-2a2 |
| x |
| 2(x+a)(x-a) |
| x |
令f'（x）=0，解得x=a或x=-a（舍）．
当x在（0，+∞）内变化时，f'（x），f（x）的变化情况如下：
| x | （0，a） | a | （a，+∞） |
| f'（x） | - | 0 | + |
| f（x） | ↘ | a2-2a2lna | ↗ |
（Ⅱ）证明：由（Ⅰ）知，f（x）的最小值M=a2-2a2lna．…（6分）
令g（x）=x2-2x2lnx（x＞0），则g'（x）=2x-4xlnx-2x=-4xlnx．
令g'（x）=0，解得x=1．…（8分）
当x在（0，+∞）内变化时，g'（x），g（x）的变化情况如下：
| x | （0，1） | 1 | （1，+∞） |
| g'（x） | + | 0 | - |
| g（x） | ↗ | 1 | ↘ |
因为a＞0，所以 M=a2-2a2lna≤1．…（11分）
点评：本题考查导数知识的运用，考查函数的单调性与最值，正确求导是关键．
练习册系列答案
相关题目
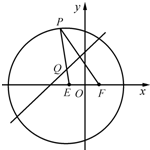如图，已知圆E：（x+1）2+y2=16，点F（1，0），P是圆E上任意一点．线段PF的垂直平分线和半径PE相交于Q．