题目内容
已知等差数列{an}的前n项和为Sn,且满足a2=4,a3+a4=17.
(1)求{an}的通项公式;
(2)设bn=2an+2,证明数列{bn}是等比数列并求其前n项和Tn.
(1)求{an}的通项公式;
(2)设bn=2an+2,证明数列{bn}是等比数列并求其前n项和Tn.
考点:等比关系的确定,等比数列的前n项和
专题:等差数列与等比数列
分析:(1)根据条件建立方程组,解首项和公差即可得到数列的通项公式.
(2)根据等比数列的定义进行证明,并能求出前n项和.
(2)根据等比数列的定义进行证明,并能求出前n项和.
解答:
解:(1)由a2=4,a3+a4=17.
得
,解得
,
∴an=3n-2.
(2)∵bn=2an+2=23n=8n,
∴
=
=8为常数,
∴数列{bn}是等比数列,公比q=8,首项b1=8,
∴Tn=
=
(8n-1).
得
|
|
∴an=3n-2.
(2)∵bn=2an+2=23n=8n,
∴
| bn |
| bn-1 |
| 8n |
| 8n-1 |
∴数列{bn}是等比数列,公比q=8,首项b1=8,
∴Tn=
| 8(1-8n) |
| 1-8 |
| 8 |
| 7 |
点评:本题主要考查等差数列和等比数列的通项公式的计算,根据条件建立方程组是解决本题的关键.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
 如图,已知椭圆C:
如图,已知椭圆C: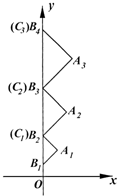 如图,在直角坐标系xOy中,有一组底边长为an的等腰直角三角形AnBnCn(n=1,2,…),底边BnCn依次放置在y轴上(相邻顶点重合),点B1的坐标为(0,b).
如图,在直角坐标系xOy中,有一组底边长为an的等腰直角三角形AnBnCn(n=1,2,…),底边BnCn依次放置在y轴上(相邻顶点重合),点B1的坐标为(0,b).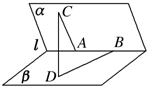 如图,在45°的二面角α-l-β的棱上有两点A、B,点C、D分别在平面 α、β内,且AC⊥AB,DB⊥AB,AC=BD=AB=1,则CD的长度为
如图,在45°的二面角α-l-β的棱上有两点A、B,点C、D分别在平面 α、β内,且AC⊥AB,DB⊥AB,AC=BD=AB=1,则CD的长度为