题目内容
空间中有一点“K”,从K放射出四条线段KA、KB、KC、KD.已知KA=3m,KB=4m,KC=5m,KD=6m.问:四面体ABCD体积的最大值是多少?
考点:棱柱、棱锥、棱台的体积
专题:综合题,空间位置关系与距离
分析:当K为四面体ABCD的“垂心”时,四面体体积最大.将四面体ABCD,扩展为正四面体,利用计算正四面体的体积,可得四面体ABCD体积的最大值.
解答:
 解:当K为四面体ABCD的“垂心”时,四面体体积最大.假设四面体ABCD体积最大时,K不是四面体的垂心.不妨设KA不垂直BCD. 然后,我们经过K向BCD划垂线,并将垂线反向延长3米,从而得到点T.显然四面体TBCD的体积大于ABCD.这就与假设矛盾了. (KB、KC、KD不垂直的证明过程与此相同) 因此,四面体ABCD体积最大时,K是四面体的垂心.
解:当K为四面体ABCD的“垂心”时,四面体体积最大.假设四面体ABCD体积最大时,K不是四面体的垂心.不妨设KA不垂直BCD. 然后,我们经过K向BCD划垂线,并将垂线反向延长3米,从而得到点T.显然四面体TBCD的体积大于ABCD.这就与假设矛盾了. (KB、KC、KD不垂直的证明过程与此相同) 因此,四面体ABCD体积最大时,K是四面体的垂心.
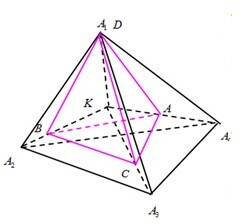
如图,DA2A3A4为正四面体,KD=KA2=KA3=KA4=6m,K为其中心,截取KA=3m,KB=4m,KC=5m,下面计算D-ABC的体积,
∵
DA2=6,∴DA2=4
,正四面体的高为h,则
h=6,∴h=3
,
∴正四面体的体积为V=
×
×(4
)2×
×3
=72
,
∴VK-DA2A3=18
,
∴VD-ABC=(
×
+
×
+
×
+
×
×
)×18
=
.
 解:当K为四面体ABCD的“垂心”时,四面体体积最大.假设四面体ABCD体积最大时,K不是四面体的垂心.不妨设KA不垂直BCD. 然后,我们经过K向BCD划垂线,并将垂线反向延长3米,从而得到点T.显然四面体TBCD的体积大于ABCD.这就与假设矛盾了. (KB、KC、KD不垂直的证明过程与此相同) 因此,四面体ABCD体积最大时,K是四面体的垂心.
解:当K为四面体ABCD的“垂心”时,四面体体积最大.假设四面体ABCD体积最大时,K不是四面体的垂心.不妨设KA不垂直BCD. 然后,我们经过K向BCD划垂线,并将垂线反向延长3米,从而得到点T.显然四面体TBCD的体积大于ABCD.这就与假设矛盾了. (KB、KC、KD不垂直的证明过程与此相同) 因此,四面体ABCD体积最大时,K是四面体的垂心.如图,DA2A3A4为正四面体,KD=KA2=KA3=KA4=6m,K为其中心,截取KA=3m,KB=4m,KC=5m,下面计算D-ABC的体积,
∵
| ||
| 4 |
| 6 |
| ||
| 3 |
| 6 |
∴正四面体的体积为V=
| 1 |
| 3 |
| 1 |
| 2 |
| 6 |
| ||
| 2 |
| 6 |
| 2 |
∴VK-DA2A3=18
| 2 |
∴VD-ABC=(
| 5 |
| 6 |
| 4 |
| 6 |
| 5 |
| 6 |
| 3 |
| 6 |
| 4 |
| 6 |
| 3 |
| 6 |
| 5 |
| 6 |
| 4 |
| 6 |
| 3 |
| 6 |
| 2 |
| 57 |
| 2 |
| 2 |
点评:本题考查四面体ABCD体积的最大值,考查学生分析解决问题的能力,确定当K为四面体ABCD的“垂心”时,四面体体积最大是关键.

练习册系列答案
相关题目
函数f(x)=(x-1)0+
的定义域为( )
| 1 | ||
|
| A、(-1,1) |
| B、(-1,+∞) |
| C、(-1,1)∪(1,+∞) |
| D、(1,+∞) |
设偶函数f(x)=
sin(2x+φ)-cos(2x+φ)(|φ|<
),则( )
| 3 |
| π |
| 2 |
A、y=f(x)的对称中心为(
| ||||||
B、y=f(x)的对称中心为(
| ||||||
C、y=f(x)的对称中心为(
| ||||||
D、y=f(x)的对称中心为(
|
已知数列{an}中,a1=1,以后各项由公式a1•a2•a3…an=n2,则a3+a5=( )
A、
| ||
B、
| ||
C、
| ||
D、
|
 在正方体ABCD-A1B1C1D1中,AA1=2,E为棱CC1的中点.
在正方体ABCD-A1B1C1D1中,AA1=2,E为棱CC1的中点.