若直线l∥平面α.直线a?α.则直线l与直线a的位置关系是( )A．l∥aB．l与a没有公共点C．l与a相交D．l与a异面题目和参考答案——青夏教育精英家教网——

题目内容

16．若直线l∥平面α，直线a?α，则直线l与直线a的位置关系是（　　）

A．

l∥a

B．

l与a没有公共点

C．

l与a相交

D．

l与a异面

分析直线l∥平面α，则有若直线l与平面α无公共点，则有直线l与直线a无公共点．

解答解：∵直线l∥平面α，
∴若直线l与平面α无公共点
又∵直线a?α
∴直线l与直线a无公共点．
故选B．

点评本题主要考查线与线的位置关系，在解题中灵活运用了公共点的个数求解．

练习册系列答案

浩鼎文化学期复习王系列答案

学年总复习假期训练营暑系列答案

学练快车道快乐假期寒假作业系列答案

学练快车道寒假同步练系列答案

学考联通学期总复习系列答案

学府图书寒假作业系列答案

学段衔接提升方案赢在高考寒假作业系列答案

新校园快乐假期系列寒假生活指导系列答案

新思维寒假作业系列答案

新路学业寒假作业快乐假期新疆青少年出版社系列答案

相关题目

6．极坐标方程ρ²cos2θ=1为所表示的曲线的离心率是$\sqrt{2}$．

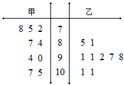某次运动会甲、乙两名射击运动员成绩如图所示，甲、乙的平均数分别为为 $\overline{{x}_{甲}}$、$\overline{{x}_{乙}}$，方差分别为s_甲²，s_乙²，则（　　）

	A．	$\overline{{x}_{甲}}$＞$\overline{{x}_{乙}}$，s_甲²＞s_乙²		B．	$\overline{{x}_{甲}}$＞$\overline{{x}_{乙}}$，s_甲²＜s_乙²
	C．	$\overline{{x}_{甲}}$＜$\overline{{x}_{乙}}$，s_甲²＞s_乙²		D．	$\overline{{x}_{甲}}$＜$\overline{{x}_{乙}}$，s_甲²＜s_乙²

4．已知f（x）是定义在R上的偶函数，它在[0，+∞）上递增，那么一定有（　　）

$f（\frac{3}{4}）＜f（{a^2}-a+1）$

$f（\frac{3}{4}）≤f（{a^2}-a+1）$

$f（\frac{3}{4}）＞f（{a^2}-a+1）$

$f（\frac{3}{4}）≥f（{a^2}-a+1）$

11．已知函数f（x）=$\frac{mx}{lnx}$，曲线y=f（x）在点（e²，f（e²））处的切线与直线2x+y=0垂直（其中e为自然对数的底数）．
（1）求f（x）的解析式及单调递减区间；
（2）若存在x₀∈[e，+∞），使函数g（x）=aelnx+$\frac{1}{2}{x^2}-\frac{a+e}{2}$•lnx•f（x）≤a成立，求实数a的取值范围．

1．已知圆x²+y²-4x+2y=0，则过圆内一点E（1，0）的最短弦长为（　　）

8．已知f（α）=$\frac{cos（\frac{π}{2}-α）•cos（2π-α）}{sin（-π-α）}$．
（I）化简f（α）；
（II）若角α为第三象限角，且f（α）=m，求tanα．

5．在△ABC中，角A，B，C所对的边分为a，b，c，向量$\overrightarrow m$=（2b-c，a），$\overrightarrow n$=（cosC，cosA），且$\overrightarrow m∥\overrightarrow n$．
（1）求角A的大小；
（2）若$\overrightarrow{AB}•\overrightarrow{AC}$=4，求边a的最小值．

6．设集合A={x|x＞-1}，B={x|-2＜x＜2}，则集合A∩B等于{x|-1＜x＜2}．