题目内容

已知函数f（x）=4x2-mx-8在[5，20]具有单调性，则实数的取值范围为（　　）
A、（-∞，-160]∪[160，+∞）
B、（-∞，40]∪[160，+∞）
C、（-∞，-160]∪[40，+∞）
D、[40，160]
考点：二次函数的性质
专题：函数的性质及应用
分析：已知函数f（x）=4x2-kx-8，求出其对称轴x=-
b
2a
，要求f（x）在〔5，20〕上具有单调性，只要对称轴x≤5，或x≥20，即可，从而求出k的范围；
解答： 解：∵函数f（x）=4x2-mx-8的对称轴为：x=-
b
2a
=-
-m
2×4
=
m
8
，
∵函数f（x）=4x2-mx-8在〔5，20〕上具有单调性，
根据二次函数的性质可知对称轴x=
m
8
≤5，或x=
m
8
≥20
∴m≤40，或m≥160
∴m∈（-∞，40〕∪〔160，+∞），
故选B．
点评：此题主要考查二次函数的图象及其性质，利用对称轴在区间上移动得出，f（x）在（5，20）上具有单调性的条件，此题是一道基础题
练习册系列答案
相关题目
一家公司计划生产某种小型产品的月固定成本为1万元，每生产1万件需要再投入2万元，设该公司一个月内生产该小型产品x万件并全部销售完，每万件的销售收入为4-x万元，且每万件国家给予补助2e-
2elnx
x
-
1
x
万元．（e为自然对数的底数，e是一个常数）
（Ⅰ）写出月利润f（x）（万元）关于月产量x（万件）的函数解析式
（Ⅱ）当月产量在[1，2e]万件时，求该公司在生产这种小型产品中所获得的月利润最大值（万元）及此时的月生成量值（万件）．（注：月利润=月销售收入+月国家补助-月总成本）
椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的离心率为
2
2
，两个焦点分别为F1（-1，0），F2（1，0）．
（1）求椭圆C的方程；
（2）过点F2（1，0）的直线l交椭圆C于M，N两点，设点N关于x轴的对称点为Q（M、Q不重合），求证：直线MQ过x轴上一个定点．
一个几何体的直观图及三视图如图所示，M，N分别是AF，BC的中点．

（Ⅰ）写出这个几何体的名称；
（Ⅱ）求证：MN∥平面CDEF；
（Ⅲ）求多面体A-CDEF的体积．
已知命题p：对?x∈R，ax2+5＞0，命题q：2x2+x-1＞0，若命题p∨q为真命题，则实数x的取值范围为
 
．
如图，在△ABC中，∠A=60°，∠A的平分线交BC于D，若AB=4，且
AD
=
1
4
AC
+
λ
AB
（λ∈R），则AD的长为
 
．
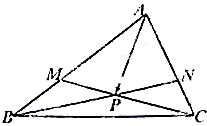在△ABC中，点M、N分别在边AB、AC上，且
AM
=2
MB
，
AN
=
3
5
AC
，线段CM与BN相交于点P，且
AB
=
a
，
AC
=
b
，则
AP
用
a
和
b
表示为（　　）
A、
AP
=
4
9
a
+
1
3
b
B、
AP
=
4
9
a
+
2
3
b
C、
AP
=
2
9
a
+
4
3
b
D、
AP
=
4
7
a
+
3
7
b
过原点的直线交双曲线xy=
2
于P、Q两点，现将坐标平面沿x轴折成直二面角，则折后线段PQ的长度的最小值等于（　　）
A、4
B、2
2
C、2
D、
2
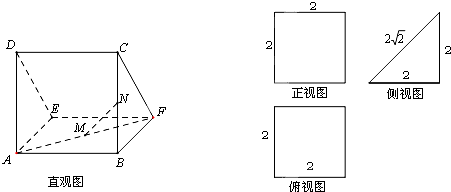
空间几何体的三视图如图所示，则该几何体的体积为（　　）
A、4+
2
3
3
B、4π+2
3
C、2π+
2
3
π
3
D、2π+
3
π
3

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网