题目内容
设函数f(x)=
-
,[x]表示不超过x的最大整数,则函数y=[f(x)]的值域是 .
| 2x |
| 1+2x |
| 1 |
| 2 |
考点:指数函数的定义、解析式、定义域和值域
专题:函数的性质及应用
分析:把函数f(x)的解析式变形,根据指数函数的值域和反比例函数的单调性求出函数f(x)的值域,利用[x]表示不超过x的最大整数求出本题的答案.
解答:
解:f(x)=
-
=
-
,
∵2x>0,∴1+2x>1,0<
<1,
∴-
<f(x)<
;
∵[x]表示不超过x的最大整数,
∴y=[f(x)]的值域为{-1,0}.
故答案为:{-1,0}.
| 2x |
| 1+2x |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 1+2x |
∵2x>0,∴1+2x>1,0<
| 1 |
| 1+2x |
∴-
| 1 |
| 2 |
| 1 |
| 2 |
∵[x]表示不超过x的最大整数,
∴y=[f(x)]的值域为{-1,0}.
故答案为:{-1,0}.
点评:本题考查了函数值域的求法,解题时应利用指数函数的值域与复合函数的单调性求解,是基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
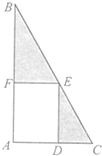 某学校计划在一块直角三角形ABC的空地上修建一个占地面积为S的矩形ADEF健身场地,如图,A=
某学校计划在一块直角三角形ABC的空地上修建一个占地面积为S的矩形ADEF健身场地,如图,A=