题目内容
若数列{an}满足a1=2,an+1=
(n∈N*),则该数列的前2014项的乘积a1•a2•a3•…a2014= .
| 1+an |
| 1-an |
考点:数列递推式
专题:计算题,等差数列与等比数列
分析:先由递推关系式,分析得到数列{an}的规律.即数列是以4为循环的数列,再求解.
解答:
解:由递推关系式,得an+2=-
,an+4=an.
∴{an}是以4为循环的一个数列.
由计算,得a1=2,a2=-3,a3=-
,a4=
,a5=2,…
∴a1a2a3a4=1,
∴a1•a2…a2010•a2014=1×a2013•a2014=a1•a2=-6.
故答案为:-6.
| 1 |
| an |
∴{an}是以4为循环的一个数列.
由计算,得a1=2,a2=-3,a3=-
| 1 |
| 2 |
| 1 |
| 3 |
∴a1a2a3a4=1,
∴a1•a2…a2010•a2014=1×a2013•a2014=a1•a2=-6.
故答案为:-6.
点评:递推关系式是数列内部之间关系的一个式子.当遇到如题中的连续多项计算,特别是不可能逐一计算时,往往数列本身会有一定的规律,如循环等,再利用规律求解.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
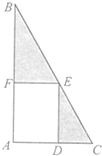 某学校计划在一块直角三角形ABC的空地上修建一个占地面积为S的矩形ADEF健身场地,如图,A=
某学校计划在一块直角三角形ABC的空地上修建一个占地面积为S的矩形ADEF健身场地,如图,A=