题目内容
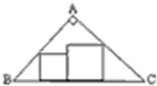 从等腰直角三角形纸片ABC上,剪下如图所示的两个正方形,其中BC=4,∠A=90°,则这两个正方形的面积之和的最小值为
从等腰直角三角形纸片ABC上,剪下如图所示的两个正方形,其中BC=4,∠A=90°,则这两个正方形的面积之和的最小值为考点:基本不等式
专题:不等式的解法及应用
分析:根据△ABC是等腰直角三角形,四边形DEGH、四边形EFNM都是正方形,可得△BDH、△CFN都是等腰直角三角形,因此可设BD=HD=x,FC=NF=y,可知x+y=1,且两个正方形的面积和为x2+y2,利用基本不等式可得面积之和的最小值.
解答:
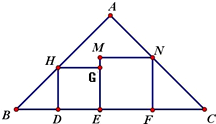 解:设HD=x,NF=y
解:设HD=x,NF=y
根据△ABC是等腰直角三角形,四边形DEGH、四边形EFNM都是正方形,可得BD=HD=x,FC=NF=y
因此BC=2BD+2FC=2,得出x+y=1
两个正方形的面积之和等于x2+y2
且 x2+y2≥(
)2=
故当且仅当x=y=
时,面积之和的最小值为
故答案为:
 解:设HD=x,NF=y
解:设HD=x,NF=y 根据△ABC是等腰直角三角形,四边形DEGH、四边形EFNM都是正方形,可得BD=HD=x,FC=NF=y
因此BC=2BD+2FC=2,得出x+y=1
两个正方形的面积之和等于x2+y2
且 x2+y2≥(
| x+y |
| 2 |
| 1 |
| 2 |
故当且仅当x=y=
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:本题考查运用基本不等式处理二元函数的最值问题,属于中档题.认准图形中的几何关系,找出其中的等量关系,建立关系式,是解决本题的关键.

练习册系列答案
相关题目
甲、乙、丙三人值周一至周六的班,每人值两天班,若甲不值周一、乙不值周六,则可排出不同的值班表数为( )
| A、30 | B、42 | C、48 | D、60 |
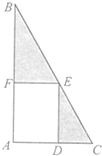 某学校计划在一块直角三角形ABC的空地上修建一个占地面积为S的矩形ADEF健身场地,如图,A=
某学校计划在一块直角三角形ABC的空地上修建一个占地面积为S的矩形ADEF健身场地,如图,A=