题目内容
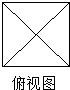一个几何体的主视图和左视图都是边长为2的等边三角形，俯视图如图所示，则这个几何体的体积为考点：由三视图求面积、体积
专题：空间位置关系与距离
分析：由已知中个几何体的主视图和左视图都是边长为2的等边三角形，结合俯视图为正方形，可得该几何体是一个四棱锥，求出底面面积和高，代入棱锥体积公式，可得答案．
解答：
解：由已知可得：该几何体是一个四棱锥，
底面棱长为2，故底面面积S=2×2=4，
高h=
×2=
，
故棱锥的体积V=
Sh=
，
故答案为：
底面棱长为2，故底面面积S=2×2=4，
高h=
| ||
| 2 |
| 3 |
故棱锥的体积V=
| 1 |
| 3 |
4
| ||
| 3 |
故答案为：
4
| ||
| 3 |
点评：本题考查了由三视图求几何体的体积，根据三视图判断几何体的结构特征及求相关几何量的数据是解答本题的关键．
练习册系列答案
相关题目
已知集合A={x|x2-2x-3=0}，集合B={x|mx+1=0}，若B⊆A，则实数m的集合为（ ）
A、{-
| ||
| B、{1} | ||
C、{-
| ||
D、{0，-
|
函数f（x）=-x3+3x在区间（a2-12，a）上有最小值，则实数a的取值范围是（ ）
A、（-1，
| ||
| B、（-1，2） | ||
| C、（-1，2] | ||
| D、（1，4） |
用秦九韶算法计算多项式f（x）=12+35x-8x2+79x3+6x4+5x5+3x6在x=-4时的值时，V2的值为（ ）
| A、-845 | B、220 |
| C、-57 | D、34 |
在△ABC中，a=2，b=6，C=60°，则三角形的面积S=（ ）
A、3
| ||
B、3
| ||
C、6
| ||
| D、6 |