题目内容
等比数列{an}的前n项和为Sn，若S2n=3（a1+a3+…+a2n-1），a1a2a3=8，则a10等于 ．
考点：等比数列的前n项和
专题：等差数列与等比数列
分析：由等比数列的性质可得a2=2，由可得公比q=2，由通项公式可得．
解答：
解：由等比数列的性质可得a1a2a3=a23=8，解得a2=2，
又∵S2n=3（a1+a3+…+a2n-1），
∴（a1+a3+…+a2n-1）+（a2+a4+…+a2n）=3（a1+a3+…+a2n-1），
∴a2+a4+…+a2n=2（a1+a3+…+a2n-1），
∴等比数列{an}的公比q=2，
∴a10=a2•q8=29=512
故答案为：512
又∵S2n=3（a1+a3+…+a2n-1），
∴（a1+a3+…+a2n-1）+（a2+a4+…+a2n）=3（a1+a3+…+a2n-1），
∴a2+a4+…+a2n=2（a1+a3+…+a2n-1），
∴等比数列{an}的公比q=2，
∴a10=a2•q8=29=512
故答案为：512
点评：本题考查等比数列的求和公式和性质，属基础题．
练习册系列答案
名校课堂系列答案
相关题目
如图，在平面四边形ABCD中，AD=1，CD=2，AC=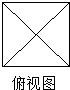
一个几何体的主视图和左视图都是边长为2的等边三角形，俯视图如图所示，则这个几何体的体积为设a=（
）
，b=（
）
，c=（
）
，则a、b、c的大小关系是（ ）
| 2 |
| 7 |
| 2 |
| 7 |
| 2 |
| 7 |
| 3 |
| 7 |
| 3 |
| 7 |
| 2 |
| 7 |
| A、a＞c＞b |
| B、a＞b＞c |
| C、c＞a＞b |
| D、b＞c＞a |