题目内容
若非零函数f(x)对任意实数a,b均有f(a+b)=f(a)•f(b),且当x<0时,f(x)>1.
(1)求证:f(x)>0;
(2)求证:f(x)为减函数;
(3)当f(4)=
时,解不等式f(x-3)•f(5)≤
.
(1)求证:f(x)>0;
(2)求证:f(x)为减函数;
(3)当f(4)=
| 1 |
| 16 |
| 1 |
| 4 |
考点:抽象函数及其应用
专题:计算题,函数的性质及应用
分析:(1)f(x)=f(
+
)=f2(
),结合函数f(x)为非零函数可得;
(2)利用函数的单调性的定义证明;
(3)由f(4)=
可得f(2)=
,从而化简不等式f(x-3)•f(5)≤
为f(x-3+5)≤f(2),从而利用单调性求解.
| x |
| 2 |
| x |
| 2 |
| x |
| 2 |
(2)利用函数的单调性的定义证明;
(3)由f(4)=
| 1 |
| 16 |
| 1 |
| 4 |
| 1 |
| 4 |
解答:
解:(1)证明:f(x)=f(
+
)=f2(
)>0,
(2)证明:∵f(0)=f2(0),∴f(0)=1;
∴f(b-b)=f(b)•f(-b)=1;
∴f(-b)=
;
任取x1<x2,则x1-x2<0,
∴
=f(x1-x2)>1,
又∵f(x)>0恒成立,
∴f(x1)>f(x2);
则f(x)为减函数;
(3)由f(4)=f2(2)=
,则f(2)=
,
原不等式转化为f(x-3+5)≤f(2),
结合(2)得:x+2≥2,
∴x≥0;
故不等式的解集为{x|x≥0}.
| x |
| 2 |
| x |
| 2 |
| x |
| 2 |
(2)证明:∵f(0)=f2(0),∴f(0)=1;
∴f(b-b)=f(b)•f(-b)=1;
∴f(-b)=
| 1 |
| f(b) |
任取x1<x2,则x1-x2<0,
∴
| f(x1) |
| f(x2) |
又∵f(x)>0恒成立,
∴f(x1)>f(x2);
则f(x)为减函数;
(3)由f(4)=f2(2)=
| 1 |
| 16 |
| 1 |
| 4 |
原不等式转化为f(x-3+5)≤f(2),
结合(2)得:x+2≥2,
∴x≥0;
故不等式的解集为{x|x≥0}.
点评:本题考查了函数单调性的证明与应用,属于中档题.

练习册系列答案
相关题目
拟定从甲地到乙地通话m分钟的话费符合f(m)=
,其中[m]表示不超过m的最大整数,从甲地到乙地通话5.2分钟的话费是( )
|
| A、4.77 | B、4.24 |
| C、3.71 | D、7.95 |
已知等比数列{an}的前三项为1,2,4,则a6=( )
| A、8 | B、32 | C、16 | D、64 |
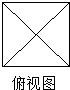 一个几何体的主视图和左视图都是边长为2的等边三角形,俯视图如图所示,则这个几何体的体积为
一个几何体的主视图和左视图都是边长为2的等边三角形,俯视图如图所示,则这个几何体的体积为