题目内容
函数f（x）=-x3+3x在区间（a2-12，a）上有最小值，则实数a的取值范围是（ ）
A、（-1，
| ||
| B、（-1，2） | ||
| C、（-1，2] | ||
| D、（1，4） |
考点：利用导数求闭区间上函数的最值
专题：函数的性质及应用
分析：求函数f（x）=-x3+3x的导数，研究其最小值取到的位置，由于函数在区间（a2-12，a）上有最小值，故最小值点的横坐标是集合（a2-12，a）的元素，由此可以得到关于参数a的等式，解之求得实数a的取值范围
解答：
解：解：由题 f'（x）=3-3x2，
令f'（x）＞0解得-1＜x＜1；令f'（x）＜0解得x＜-1或x＞1
由此得函数在（-∞，-1）上是减函数，在（-1，1）上是增函数，在（1，+∞）上是减函数，
∵f（0）=0，∴函数f（x）=-x3+3x在R上的图象大体如下：
故函数在x=-1处取到极小值-2，判断知此极小值必是区间（a2-12，a）上的最小值
∴a2-12＜-1＜a，解得-1＜a＜
，
又当x=2时，f（2）=-2，故有a≤2
综上知a∈（-1，2]
故选：C．
令f'（x）＞0解得-1＜x＜1；令f'（x）＜0解得x＜-1或x＞1
由此得函数在（-∞，-1）上是减函数，在（-1，1）上是增函数，在（1，+∞）上是减函数，
∵f（0）=0，∴函数f（x）=-x3+3x在R上的图象大体如下：
故函数在x=-1处取到极小值-2，判断知此极小值必是区间（a2-12，a）上的最小值
∴a2-12＜-1＜a，解得-1＜a＜
| 11 |
又当x=2时，f（2）=-2，故有a≤2
综上知a∈（-1，2]
故选：C．
点评：本题考查用导数研究函数的最值，利用导数研究函数的最值是导数作为数学中工具的一个重要运用，要注意把握其作题步骤，求导，确定单调性，得出最值．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图，在平面四边形ABCD中，AD=1，CD=2，AC=拟定从甲地到乙地通话m分钟的话费符合f（m）=
，其中[m]表示不超过m的最大整数，从甲地到乙地通话5.2分钟的话费是（ ）
|
| A、4.77 | B、4.24 |
| C、3.71 | D、7.95 |
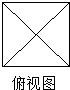一个几何体的主视图和左视图都是边长为2的等边三角形，俯视图如图所示，则这个几何体的体积为