题目内容
已知集合A={x|x2-2x-3=0},集合B={x|mx+1=0},若B⊆A,则实数m的集合为( )
A、{-
| ||
| B、{1} | ||
C、{-
| ||
D、{0,-
|
考点:集合的包含关系判断及应用
专题:计算题,集合
分析:由题意,化简A={x|x2-2x-3=0}={-1,3},结合方程mx+1=0可知B为∅,{-1},{3},从而解得.
解答:
解:A={x|x2-2x-3=0}={-1,3},
①若m=0,则B=∅,成立;
②若-m+1=0,则m=1;
③若3m+1=0,则m=-
;
故选D.
①若m=0,则B=∅,成立;
②若-m+1=0,则m=1;
③若3m+1=0,则m=-
| 1 |
| 3 |
故选D.
点评:本题考查了集合的包含关系的应用,同时考查了分类讨论的数学思想,属于基础题.

练习册系列答案
相关题目
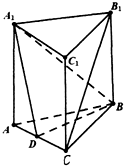 在直三棱柱中,AA1=AB=BC=3,AC=2,D是AC中点.
在直三棱柱中,AA1=AB=BC=3,AC=2,D是AC中点. 如图,在平面四边形ABCD中,AD=1,CD=2,AC=
如图,在平面四边形ABCD中,AD=1,CD=2,AC=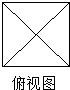 一个几何体的主视图和左视图都是边长为2的等边三角形,俯视图如图所示,则这个几何体的体积为
一个几何体的主视图和左视图都是边长为2的等边三角形,俯视图如图所示,则这个几何体的体积为