题目内容
已知双曲线x2-
=1的右焦点与抛物线y2=8x的焦点重合,则它的焦点到其渐近线的距离为 .
| y2 |
| b2 |
考点:抛物线的简单性质,双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:可求得抛物线y2=8x的焦点坐标,从而可求得b2及双曲线的右焦点坐标,利用点到直线间的距离公式即可.
解答:
解:∵抛物线y2=8x的焦点坐标为(2,0),
依题意,1+b2=4,
∴b2=3.
∴双曲线的渐近线方程为:y=±
x,
∴双曲线的一个焦点F(2,0)到其渐近线的距离等于d=
.
故答案为:
.
依题意,1+b2=4,
∴b2=3.
∴双曲线的渐近线方程为:y=±
| 3 |
∴双曲线的一个焦点F(2,0)到其渐近线的距离等于d=
| 3 |
故答案为:
| 3 |
点评:本题考查双曲线的简单性质,求得b2的值是关键,考查点到直线间的距离公式,属于中档题.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
拟定从甲地到乙地通话m分钟的话费符合f(m)=
,其中[m]表示不超过m的最大整数,从甲地到乙地通话5.2分钟的话费是( )
|
| A、4.77 | B、4.24 |
| C、3.71 | D、7.95 |
复数Z=2+arcsinx+(π-3)xi,(x∈R,i是虚数单位),在复平面上的对应点只可能位于 ( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
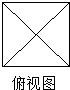 一个几何体的主视图和左视图都是边长为2的等边三角形,俯视图如图所示,则这个几何体的体积为
一个几何体的主视图和左视图都是边长为2的等边三角形,俯视图如图所示,则这个几何体的体积为