题目内容
已知点A(0,2)和圆C:(x-6)2+(y-4)2=
,一条光线从A点出发射到x轴上后沿圆的切线方向反射,求:
(1)这条光线从A点到切点所经过的路程.
(2)求入射光线的方程.
| 36 |
| 5 |
(1)这条光线从A点到切点所经过的路程.
(2)求入射光线的方程.
考点:直线与圆的位置关系,圆的切线方程
专题:直线与圆
分析:(1)先求A的对称点的坐标,设反射线斜率,利用相切求出斜率,可得方程,这条光线从A点到切点所经过的路程.可以求对称点到切点的距离即可.
(2)入射光线与反射光线斜率相反,纵截距相反,结合(1)中反射光线的方程,可得答案.
(2)入射光线与反射光线斜率相反,纵截距相反,结合(1)中反射光线的方程,可得答案.
解答:
 解:如图所示,设A关于x轴的对称点为A′,则A′(0,-2).
解:如图所示,设A关于x轴的对称点为A′,则A′(0,-2).
由光学性质可知,A′在反射线上,可设反射线方程为y=kx-2.
因为反射线与圆相切,所以
=
,
解得k1=2,k2=
,于是,反射线方程为2x-y-2=0与x-2y-4=0.
设切点为M,反射点为B,则|AB|+|BM|=|A′B|+|BM|=|A′M|=
=
(2)∵射光线与反射光线斜率相反,纵截距相反,
可得:k3=-2,k4=-
,b=2,
即入射光线的方程为y=-2x+2,y=-
x+2,
即2x+y-2=0或x+2y-4=0.
 解:如图所示,设A关于x轴的对称点为A′,则A′(0,-2).
解:如图所示,设A关于x轴的对称点为A′,则A′(0,-2).由光学性质可知,A′在反射线上,可设反射线方程为y=kx-2.
因为反射线与圆相切,所以
| |6k-4-2| | ||
|
| 6 | ||
|
解得k1=2,k2=
| 1 |
| 2 |
设切点为M,反射点为B,则|AB|+|BM|=|A′B|+|BM|=|A′M|=
|A′C|2-(
|
18
| ||
| 5 |
(2)∵射光线与反射光线斜率相反,纵截距相反,
可得:k3=-2,k4=-
| 1 |
| 2 |
即入射光线的方程为y=-2x+2,y=-
| 1 |
| 2 |
即2x+y-2=0或x+2y-4=0.
点评:本题考查直线与圆的位置关系,点、直线对称的圆的方程,是中档题.

练习册系列答案
相关题目
五名同学在“爱心捐助”活动中,捐款数额为8,10,10,4,6(单位:元),这组数据的中位数是( )
| A、10 | B、9 | C、8 | D、6 |
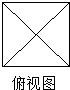 一个几何体的主视图和左视图都是边长为2的等边三角形,俯视图如图所示,则这个几何体的体积为
一个几何体的主视图和左视图都是边长为2的等边三角形,俯视图如图所示,则这个几何体的体积为