题目内容
（1）如果α是第一象限角，那么
是第几象限角？
（2）如果α是第二象限角，判断
的符号．
| α |
| 3 |
（2）如果α是第二象限角，判断
| sin(cosα) |
| cos(sinα) |
考点：三角函数值的符号,象限角、轴线角
专题：三角函数的求值
分析：（1）根据第一象限的角的不等式表示，列出不等关系2kπ＜α＜2kπ+
，k∈Z，再利用不等式的基本性质，两边同除以3，求出
的不等关系，从而判断出
是第几象限的角．
（2）通过角所在象限，通过三角函数值的符号，判断结果即可．
| π |
| 2 |
| α |
| 3 |
| α |
| 3 |
（2）通过角所在象限，通过三角函数值的符号，判断结果即可．
解答：
解：（1）∵2kπ＜α＜2kπ+
，k∈Z，
∴
＜
＜
+
，k∈Z，
当k=3n（n∈Z）时，2nπ＜
＜2nπ+
，n∈Z，
是第一象限的角，
当k=3n+1（n∈Z）时，2nπ+
＜
＜2nπ+
，n∈Z，
是第二象限的角，
当k=3n+2（n∈Z）时，2nπ+
＜
＜2nπ+
，n∈Z，
是第三象限的角．
∴
是第一，二，三象限的角．
（2）α是第二象限角，sinα∈（0，1），cosα∈（-1，0）．
∴cos（sinα）＞0，sin（cosα）＜0，
∴
＜0．
| π |
| 2 |
∴
| 2kπ |
| 3 |
| α |
| 3 |
| 2kπ |
| 3 |
| π |
| 6 |
当k=3n（n∈Z）时，2nπ＜
| α |
| 3 |
| π |
| 6 |
| α |
| 3 |
当k=3n+1（n∈Z）时，2nπ+
| 2π |
| 3 |
| α |
| 3 |
| 5π |
| 6 |
| α |
| 3 |
当k=3n+2（n∈Z）时，2nπ+
| 4π |
| 3 |
| α |
| 3 |
| 3π |
| 2 |
| α |
| 3 |
∴
| α |
| 3 |
（2）α是第二象限角，sinα∈（0，1），cosα∈（-1，0）．
∴cos（sinα）＞0，sin（cosα）＜0，
∴
| sin(cosα) |
| cos(sinα) |
点评：本题主要考查了象限角、轴线角，三角函数值的符号的判断，属于基础题．
练习册系列答案
新卷王期末冲刺100分系列答案
全能闯关100分系列答案
相关题目
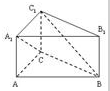已知直三棱柱ABC--A1B1C1中，AB=4，AC=AA1=2，∠ACB=90°．