题目内容
已知椭圆
+
=1(a>b>0)的左、右顶点分别为A、B.椭圆长半轴的长为2,离心率为e=
.
(1)求椭圆的方程;
(2)设点P在直线上x=4不同于点(4,0)的任意一点,若直线AP、BP分别与椭圆相交于异于A、B的点M、N,证明:点B在以MN为直径的圆内.
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
(1)求椭圆的方程;
(2)设点P在直线上x=4不同于点(4,0)的任意一点,若直线AP、BP分别与椭圆相交于异于A、B的点M、N,证明:点B在以MN为直径的圆内.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)由已知得
,由此能求出椭圆方程.
(2)A(-2,0),B(2,0),设M(x0,y0),则y02=
(4-x02),-2<x0<2,由已知条件推导出
•
>0,由此能证明点B在以MN为直径的圆内.
|
(2)A(-2,0),B(2,0),设M(x0,y0),则y02=
| 3 |
| 4 |
| BM |
| BP |
解答:
(1)解:∵椭圆
+
=1(a>b>0)的左、右顶点分别为A、B.
椭圆长半轴的长为2,离心率为e=
,
∴
,解得a=2,c=1,b=
=
,
∴椭圆方程为
+
=1.
(2)证明:由(Ⅰ)得A(-2,0),B(2,0),设M(x0,y0),
∵M点在椭圆上,
∴y02=
(4-x02),①
又点M异于顶点A、B,
∴-2<x0<2,
由P、A、M三点共线可以得 P(4,
),
从而
=(x0 -2,y0),
=(2,
),
∴
•
=2x0-4+
=
(x02-4+3y02),②
将①代入②,化简得
•
=
(2-x0),
∵2-x0>0,
∴
•
>0,则∠MBP为锐角,从而∠MBN为钝角,
故点B在以MN为直径的圆内.
| x2 |
| a2 |
| y2 |
| b2 |
椭圆长半轴的长为2,离心率为e=
| 1 |
| 2 |
∴
|
| 4-1 |
| 3 |
∴椭圆方程为
| x2 |
| 4 |
| y2 |
| 3 |
(2)证明:由(Ⅰ)得A(-2,0),B(2,0),设M(x0,y0),
∵M点在椭圆上,
∴y02=
| 3 |
| 4 |
又点M异于顶点A、B,
∴-2<x0<2,
由P、A、M三点共线可以得 P(4,
| 6y0 |
| x0+2 |
从而
| BM |
| BP |
| 6y0 |
| x0+2 |
∴
| BM |
| BP |
| 6y02 |
| x0+2 |
| 2 |
| x0+2 |
将①代入②,化简得
| BM |
| BP |
| 5 |
| 2 |
∵2-x0>0,
∴
| BM |
| BP |
故点B在以MN为直径的圆内.
点评:本题考查椭圆方程的求法,考查点在圆内的证明,解题时要认真审题,注意椭圆、圆、直线方程、向量等知识点的合理运用.

练习册系列答案
相关题目
方程
+
=2表示( )
| (x+1)2+y2 |
| (x-1)2+y2 |
| A、椭圆 | B、圆 | C、直线 | D、线段 |
如图,在△ABC中,AB=3,AC=4,BC=5,AD平分∠BAC,则BD的值为( )
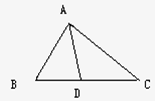

A、
| ||
B、
| ||
C、
| ||
D、
|
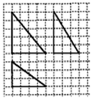 如图,格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体最长的棱的长度等于( )
如图,格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体最长的棱的长度等于( )A、
| ||
B、
| ||
C、5
| ||
D、2
|
关于x的不等式sin2x+acosx-a2≤1+cosx对一切x∈R恒成立,则实数a的取值范围为( )
A、(-1,
| ||
B、[-1,
| ||
C、(-∞,-1]∪[
| ||
D、(-∞,-1)∪(
|