题目内容
2.曲线$y={x^2}+x+\frac{1}{2}$在$({0,\frac{1}{2}})$处的切线方程为( )| A. | $y=-x+\frac{1}{2}$ | B. | $y=x+\frac{1}{2}$ | C. | $y=-2x+\frac{1}{2}$ | D. | $y=2x+\frac{1}{2}$ |
分析 欲求在点$({0,\frac{1}{2}})$处的切线方程,只须求出其斜率的值即可,故先利用导数求出在x=0处的导函数值,再结合导数的几何意义即可求出切线的斜率,从而问题解决.
解答 解:因为y′=2x+1,所以y′|x=0=1,
所以切线方程为y-$\frac{1}{2}$=x,即$y=x+\frac{1}{2}$.
故选B.
点评 本题主要考查导数的几何意义,根据条件求出对应的切线斜率是解决本题的关键.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案
相关题目
12.函数y=x2cosx的导数为( )
| A. | y′=x2cosx-2xsin x | B. | y′=2xcos x+x2sin x | ||
| C. | y′=2xcosx-x2sinx | D. | y′=xcosx-x2sin x |
13.已知复数z=1+i,则 $\frac{{{z^2}-2z}}{1-z}$=( )
| A. | 2i | B. | -2i | C. | 2 | D. | -2 |
10.已知复数z=i(1+2i),则复数z的虚部为( )
| A. | 2 | B. | 3 | C. | -1 | D. | 1 |
17.已知角α的终边经过点(m,9),且$tanα=\frac{3}{4}$,则sinα的值为( )
| A. | $\frac{4}{5}$ | B. | $-\frac{4}{5}$ | C. | $\frac{3}{5}$ | D. | $-\frac{3}{5}$ |
7.函数f(x)的导函数f′(x)的图象如图所示,则( )
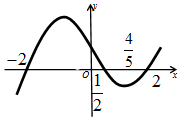

| A. | $\frac{1}{2}$为f(x)的极大值点 | B. | -2为f(x)的极大值点 | ||
| C. | 2为f(x)的极大值 | D. | $\frac{4}{5}$为f(x)的极小值点 |
14.某家公司每月生产两种布料A和B,所有原料是三种不同颜色的羊毛.下表给出了生产每匹每种布料所需的羊毛量,以及可供使用的每种颜色的羊毛的总量.
已知生产每匹布料A、B的利润分别为60元、40元.分别用x、y表示每月生产布料A、B的匹数.
(Ⅰ)用x、y列出满足生产条件的数学关系式,并画出相应的平面区域;
(Ⅱ)如何安排生产才能使得利润最大?并求出最大的利润.
| 羊毛颜色 | 每匹需要/kg | 供应量/kg | |
| 布料A | 布料B | ||
| 红 | 3 | 3 | 1050 |
| 绿 | 4 | 2 | 1200 |
| 黄 | 2 | 6 | 1800 |
(Ⅰ)用x、y列出满足生产条件的数学关系式,并画出相应的平面区域;
(Ⅱ)如何安排生产才能使得利润最大?并求出最大的利润.
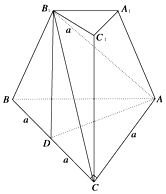 三棱台ABC-A1B1C1中,侧棱CC1⊥底面ABC,∠ACB=90°,AC=B1C1=a,BC=2a,AB1与CC1成45°角,D为BC中点,
三棱台ABC-A1B1C1中,侧棱CC1⊥底面ABC,∠ACB=90°,AC=B1C1=a,BC=2a,AB1与CC1成45°角,D为BC中点,