题目内容
15.在?ABCD中,E是CD上一点,且$\overrightarrow{AE}$=$\frac{1}{2}$$\overrightarrow{AB}$+$\overrightarrow{BC}$,AB=2BC=4,∠BAD=60°,则$\overrightarrow{AC}$•$\overrightarrow{EB}$等于( )| A. | $\frac{1}{2}$ | B. | $\frac{3}{2}$ | C. | 2 | D. | 3 |
分析 利用向量关系,转化求解向量的数量积即可.
解答 解:由$\overrightarrow{AE}$=$\frac{1}{2}$$\overrightarrow{AB}$+$\overrightarrow{BC}$,得$\overrightarrow{DE}$=$\frac{1}{2}\overrightarrow{AB}$=$\frac{1}{2}\overrightarrow{DC}$,即E是CD的中点,∵$\overrightarrow{AC}$=$\overrightarrow{AB}$$+\overrightarrow{AD}$,$\overrightarrow{EB}$=$\overrightarrow{ED}$$+\overrightarrow{DA}$$+\overrightarrow{AB}$,
∴$\overrightarrow{AC}•\overrightarrow{EB}$=($\overrightarrow{AB}$$+\overrightarrow{AD}$)($\frac{1}{2}\overrightarrow{AB}$$-\overrightarrow{AD}$)=$\frac{1}{2}{\overrightarrow{AB}}^{2}$-$\frac{1}{2}\overrightarrow{AB}•\overrightarrow{AD}$-${\overrightarrow{AD}}^{2}$=$\frac{1}{2}×4×4$$-\frac{1}{2}×4×2×\frac{1}{2}$-2×2=2.
故选:C.
点评 本题考查向量在几何中的应用,平面向量的数量积的运算,考查计算能力.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
1.下列函数既是增函数,图象又关于原点对称的是( )
| A. | y=x|x| | B. | y=ex | C. | $y=-\frac{1}{x}$ | D. | y=log2x |
2.曲线$y={x^2}+x+\frac{1}{2}$在$({0,\frac{1}{2}})$处的切线方程为( )
| A. | $y=-x+\frac{1}{2}$ | B. | $y=x+\frac{1}{2}$ | C. | $y=-2x+\frac{1}{2}$ | D. | $y=2x+\frac{1}{2}$ |
3.在等差数列{an}中,S10=120,那么a1+a10的值是( )
| A. | 12 | B. | 24 | C. | 36 | D. | 48 |
5.已知集合A={x|x2+2x<0},B={x|($\frac{1}{2}$)x-2≥0},则A∩B=( )
| A. | (-2,-1) | B. | (-1,0) | C. | (-2,-1] | D. | [-1,0) |
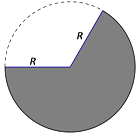 某工厂要生产体积为定值V的漏斗,现选择半径为R的圆形马口铁皮,截取如图所示的扇形,焊制成漏斗.
某工厂要生产体积为定值V的漏斗,现选择半径为R的圆形马口铁皮,截取如图所示的扇形,焊制成漏斗.