题目内容
10．已知复数z=i（1+2i），则复数z的虚部为（ ）| A． | 2 | B． | 3 | C． | -1 | D． | 1 |
分析 根据复数的概念即可得到结论
解答 解：z=i（1+2i）=-2+i，则z的虚部为1，
故选：D
点评 本题主要考查复数的有关概念，利用复数的基本运算即可得到结论．
练习册系列答案
相关题目
20．曲线y=x2+1与两坐标轴及x=1所围成的图形的面积S为（ ）
| A． | $\frac{1}{3}$ | B． | $\frac{4}{3}$ | C． | $\frac{5}{3}$ | D． | 2 |
1．下列函数既是增函数，图象又关于原点对称的是（ ）
| A． | y=x|x| | B． | y=ex | C． | $y=-\frac{1}{x}$ | D． | y=log2x |
18．要得到$y=cos（4x-\frac{π}{3}）$的图象，只需将函数y=cos4x图象（ ）
| A． | 向左平移$\frac{π}{12}$个单位 | B． | 向右平移$\frac{π}{12}$个单位 | ||
| C． | 向左平移$\frac{π}{3}$个单位 | D． | 向右平移$\frac{π}{3}$个单位 |
5．$\int_2^3{（2x+1）dx=}$（ ）
| A． | 2 | B． | 6 | C． | 10 | D． | 8 |
2．曲线$y={x^2}+x+\frac{1}{2}$在$（{0，\frac{1}{2}}）$处的切线方程为（ ）
| A． | $y=-x+\frac{1}{2}$ | B． | $y=x+\frac{1}{2}$ | C． | $y=-2x+\frac{1}{2}$ | D． | $y=2x+\frac{1}{2}$ |
3．在等差数列{an}中，S10=120，那么a1+a10的值是（ ）
| A． | 12 | B． | 24 | C． | 36 | D． | 48 |
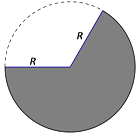某工厂要生产体积为定值V的漏斗，现选择半径为R的圆形马口铁皮，截取如图所示的扇形，焊制成漏斗．